Optical Sensitivity of TL Glow Peaks Separated Using Computerized Glow Curve Deconvolution for RTL Quartz
Article information
Abstract
Background
The retrospective dosimetry using RTL quartz can be improved by information for an optical sensitivity of sample connected with the equivalent dose determination.
Materials and Methods
The quartz sample from a volcanic rock of Japan was used. After correcting the thermal quenching effect, RTL peaks of quartz were separated by the CGCD method cooperated with the general order kinetics. The number of overlapped glow peaks were ascertained by the Tm-Tstop method. The optical sensitivity was examined by comparing the change of intensity on RTL glow peaks measured after exposure to light from a solar simulator with various illumination times.
Results and Discussion
Seven glow peaks appeared to be overlapped on the RTL glow curve. The general order kinetics model was appropriate to separate glow peaks. After exposure to light from a solar simulator from a few minutes to 416 hr, the signals for peaks P4 and P5 decayed following the form of f(t)=a1e−λ1t, while the signals for peaks P6 and P7 decayed by the form of f(t)=a1e−λ1t+a2e−λ2t+a3e−λ3t.
Conclusion
For dosimetric peaks, the times taken to reduce the RTL signal to half of its initial value were 70 sec for the peak P4, 54 s for the peak P5, 9,840 sec for the peak P6 and 26,580 sec for the peak P7, respectively. We conclude that the optical sensitivity of peaks P4, and P5 gives much higher than that of peaks P6 and P7.
Introduction
It is well known that the colours of radiation induced thermoluminescence (TL) of natural quartz typically indicate blue with an emission wavelength of around 470 nm and red with an emission wavelength of around 630 nm. The quartz annealed at high temperature, such as volcanically originated tephra layers or archaeological heated materials, shows a red TL (RTL), whereas the quartz from sediment emits a blue TL (BTL). Of two types of quartz, the RTL quartz gives some advantages in the field of retrospective dosimetry, due to much higher saturation response to radiation dose than BTL quartz and stability of the TL signal during the long timescale. Extensive research has been performed to explore the RTL characteristics [1, 2]. The methodological technique for the retrospective dosimetry can be improved by information for an optical sensitivity of sample, so called bleaching, relevant to the determination of the equivalent dose. Concerning the optical sensitivity, Scholefield and Prescott et al. [3] reported that by optical stimulation, the peak at 350°C of the natural RTL quartz reduced slowly while a rapid decrease was found in the peaks at 270°C and 305°C of some RTL quartz. Fattahi and Stokes [2] also demonstrated that natural RTL quartz was bleachable by sunlight. Later, Lai and Murray [4] found that after exposure to sunlight, the TL intensity of RTL quartz from Chinese loess was reduced but up to approximately 40% of the natural signal did not show any change. Such exploitation by the similar approach has been extensively investigated on many kinds of quartz. However, most work was carried out with the TL signal integrated for a specific temperature limits of interest in the glow curve. However, it has been suggested that the glow curve of the quartz sample is overlapped with several peaks [5, 6]. Although various techniques have been introduced to separate TL glow curve, the peak separation using the computerized glow curve deconvolution (CGCD) method has some advantages in the instance of the glow curve overlapped with several glow peaks [7].
In this work, we investigated on the optical sensitivity using a solar simulator of TL peaks separated by the CGCD method for RTL quartz of volcanic origin from Japan.
Materials and Methods
The quartz sample collected from a volcanic rock in Iwate Prefecture (Japan) was employed for this study. Isolation of the quartz was made by density between 2.60 and 2.70 g·cm−3. The quartz was treated with 40% hydrofluoric acid for 1 hour to eliminate the feldspar and then rinsed with 10% H2O2 and 10% HCl. The resulting quartz was sieved into grain size of ~125 mm and the purity of quartz sample was checked by measuring the luminescence by infrared stimulation.
An automated Riso TL/OSL system (Model TL/OSL-DA-15) in the Central Laboratory of Kangwon National University was employed for all RTL measurements. Irradiation to samples was made with a 90Sr/90Y beta source delivering approximately 0.13 Gy·s−1, which was calibrated using a standard quartz, housed in the system. The detection of RTL signal was performed by a PMT (R943-01 Hamamatsu Photonics Corp., Shizuoka, Japan) attached with a Cormar 650IU band-pass filter with a transmission range of 630–670 nm. The time independent signal was reduced using a thermoelectric refrigeration chamber (PC182CE PHOTOCOOL) maintained at 20°C.
Results and Discussion
1. Emission property of RTL quartz sample
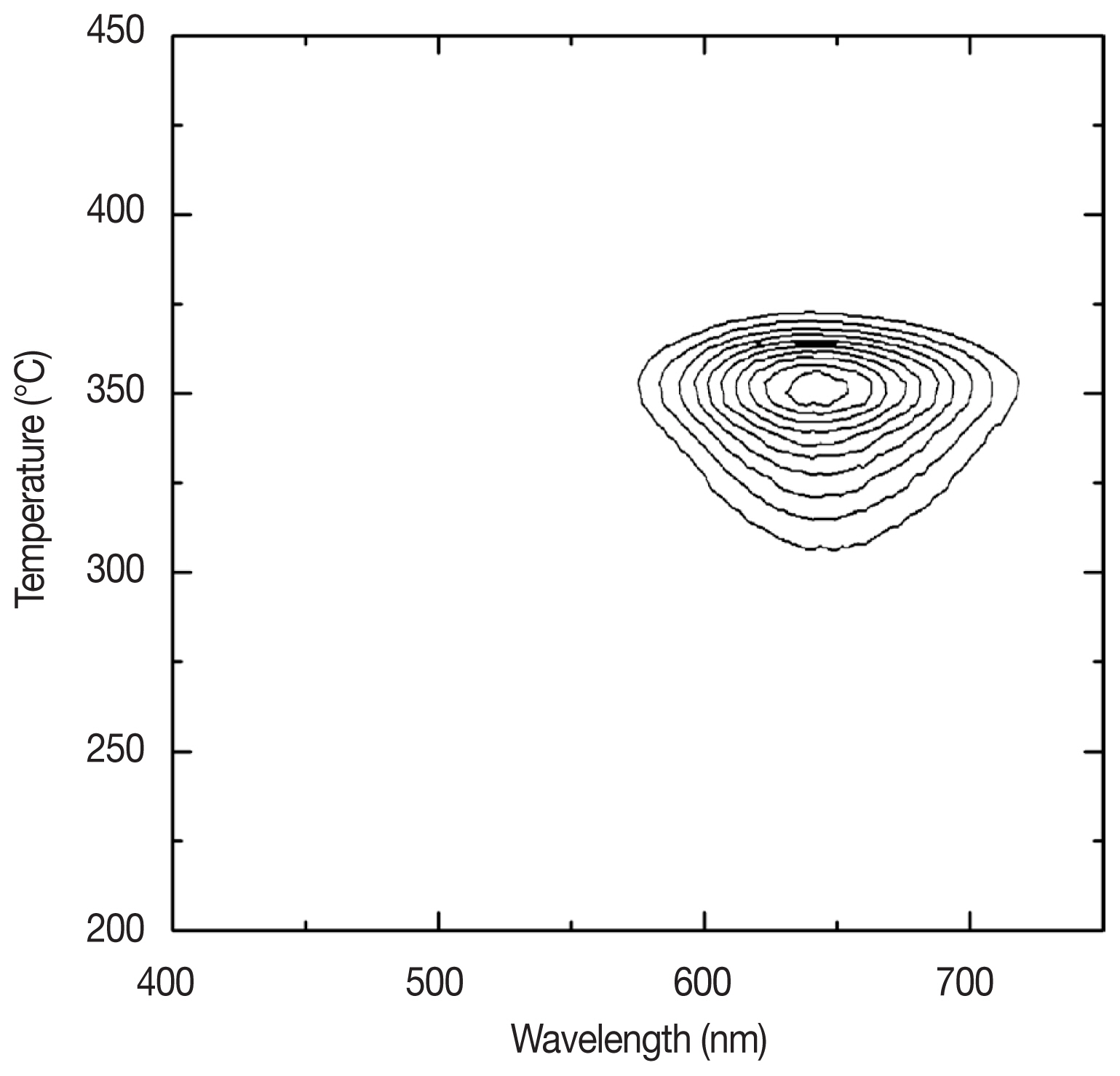
The emission wavelength of RTL quartz sample used in this study was tested by the spectral analysis using an on-line three-dimensional TL spectrometer [8]. The RTL quartz sample preheated for 60 s at 220°C after an X-ray exposure of about 2 kGy was prepared for this test. As shown in Figure 1, the spectrum clearly shows a strong emission peak in a wavelength of around 660 nm, peaking at ~350°C.
2. Thermal quenching
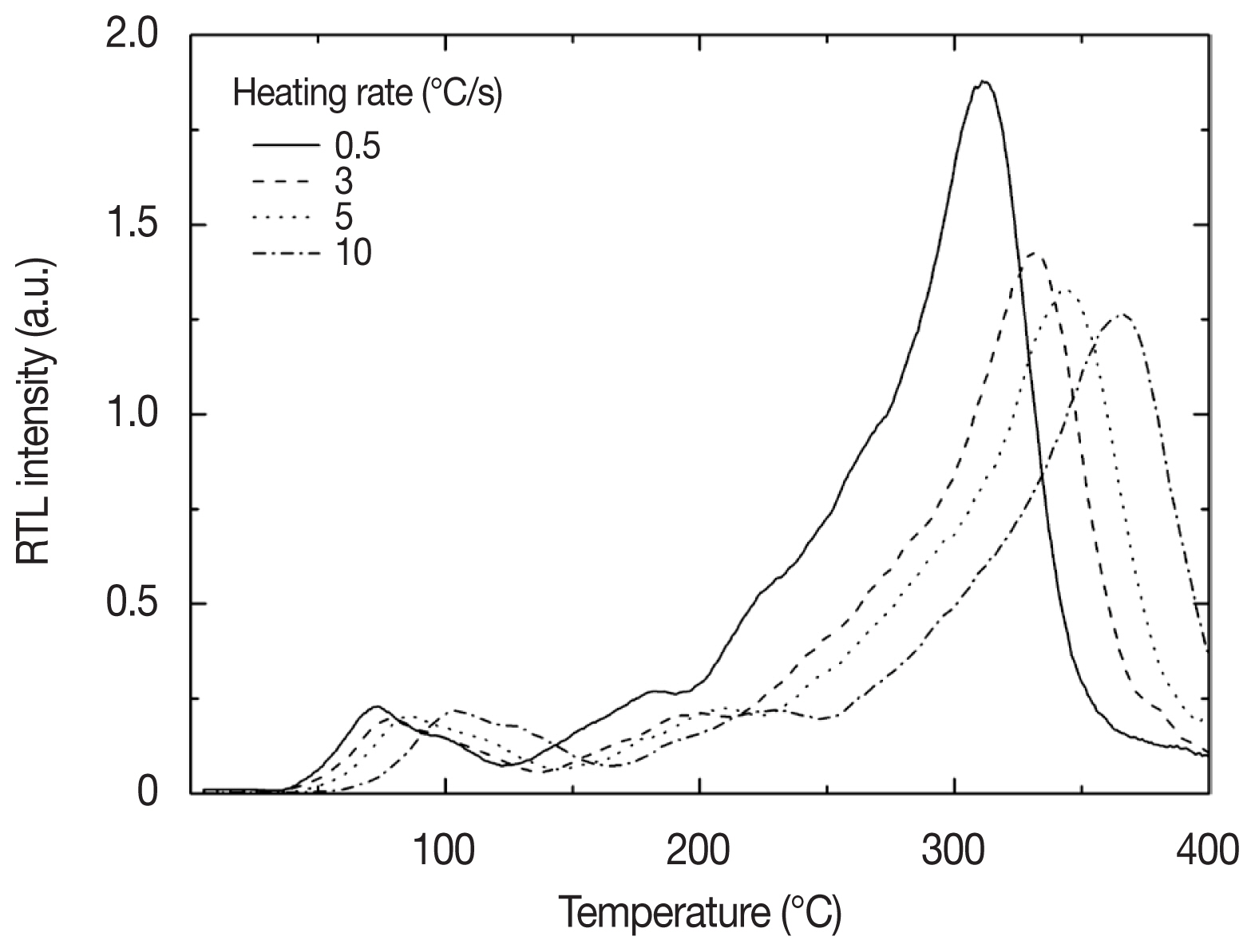
Prior to the peak separation, the checking of thermal quenching is an important process because the luminescence efficacy to radiation may change with temperature. For checking of the thermal quenching, RTL measurements were made for heating rates changing from 0.5°C·s−1 to 10°C·s−1 with the samples exposed with a beta dose of 300 Gy as shown in Figure 2. If the thermal quenching does not occur, the TL glow peak area is anticipated to be constant irrespective of the variation of heating rate. However, we observed that the area integrated at the higher temperature peaks on the glow curve clearly reduced according to the increment of heating rate, as shown in Figure 2. This suggests that the thermal quenching took place [9]. In this study we corrected the thermal quenching by means of the normalisation of RTL intensity measured for various heating rates [9]. The effect of thermal quenching is represented by the thermal quenching efficiency given by
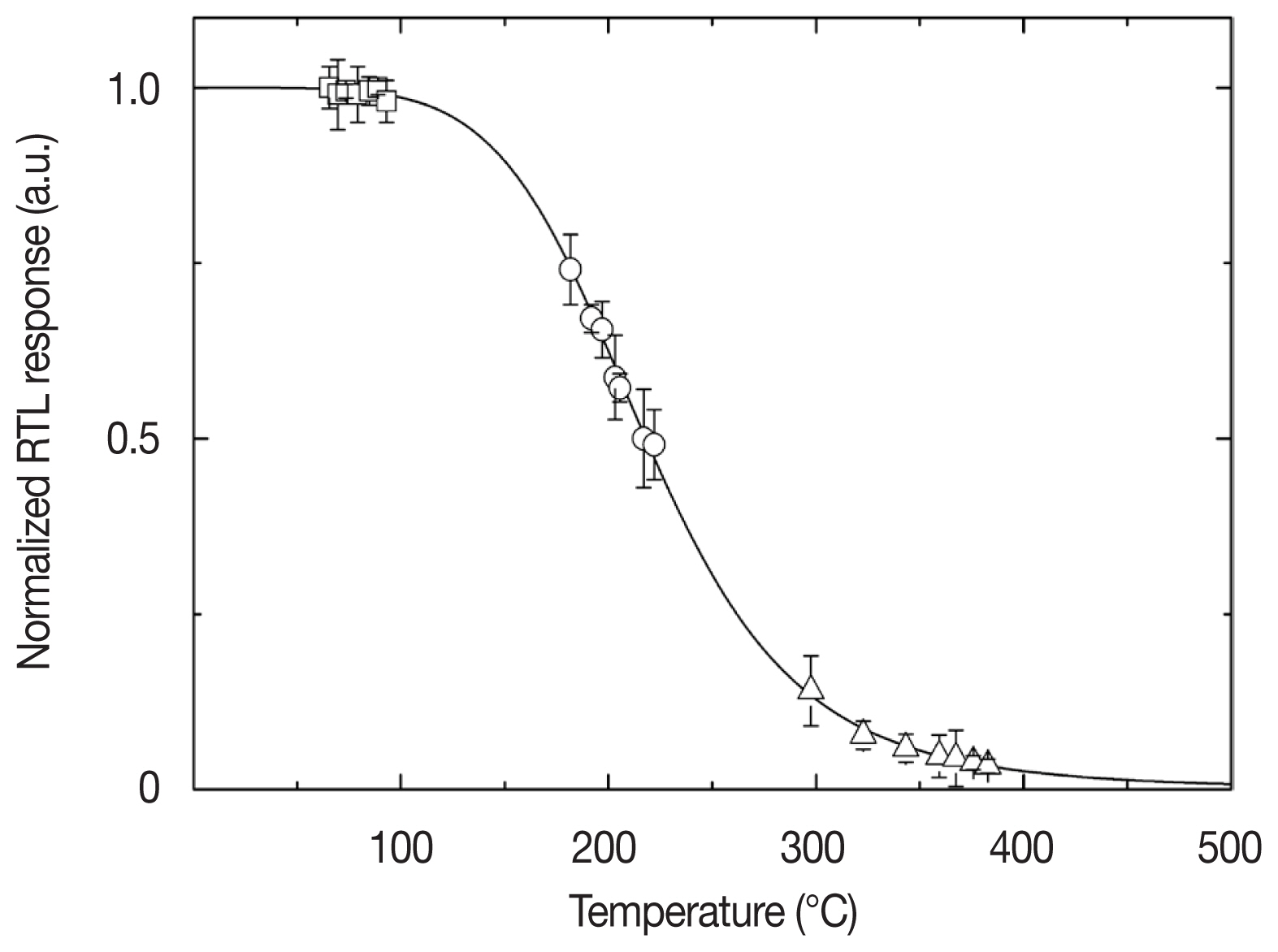
where the values of W, C, kb and T mean the thermal activation energy for thermal quenching, a constant, the Boltzmann constant and the temperature, respectively. The values of W and C are produced from the luminescence efficiency of the RTL peaks for various heating rates (Figure 3). From this procedure, the resultant values of C and W were 0.65×106 and 0.57 eV. These values are of similar to those of other RTL quartz reported in previous [10]. The thermal quenching was then corrected by
where IQ (T) is the RTL intensity after correcting the thermal quenching and IU (T) is the RTL intensity before correcting the thermal quenching.
3. Peak separation
In general, the glow curves of RTL quartz are overlapped with several peaks and can be separated by a CGCD method which is a very useful technique to obtain the information of trap in many instances. However, before the process of separation of glow curves using the CGCD method, it is essential to know the number of glow peaks overlapped on the glow curve. In this investigation, the number of glow peaks overlapped on the TL glow curve was identified using Tm-Tstop method [11]. The procedure adopted in this study is as follows. With the quartz samples exposed with a beta dose of 300 Gy, RTL measurement involving a partial heating was made to a temperature named as Tstop and then the samples were cooled to room temperature. This sequence is continued several times to all of the remaining glow curve at various temperatures (Tstop) up to 450°C with a 5°C interval. Figure 4 shows the first maximum temperatures (Tm) of remaining RTL glow curves for each initial heating temperature (Tstop). As a result, seven plateaus were found, which suggests that the RTL glow curve is overlapped with seven glow peaks.
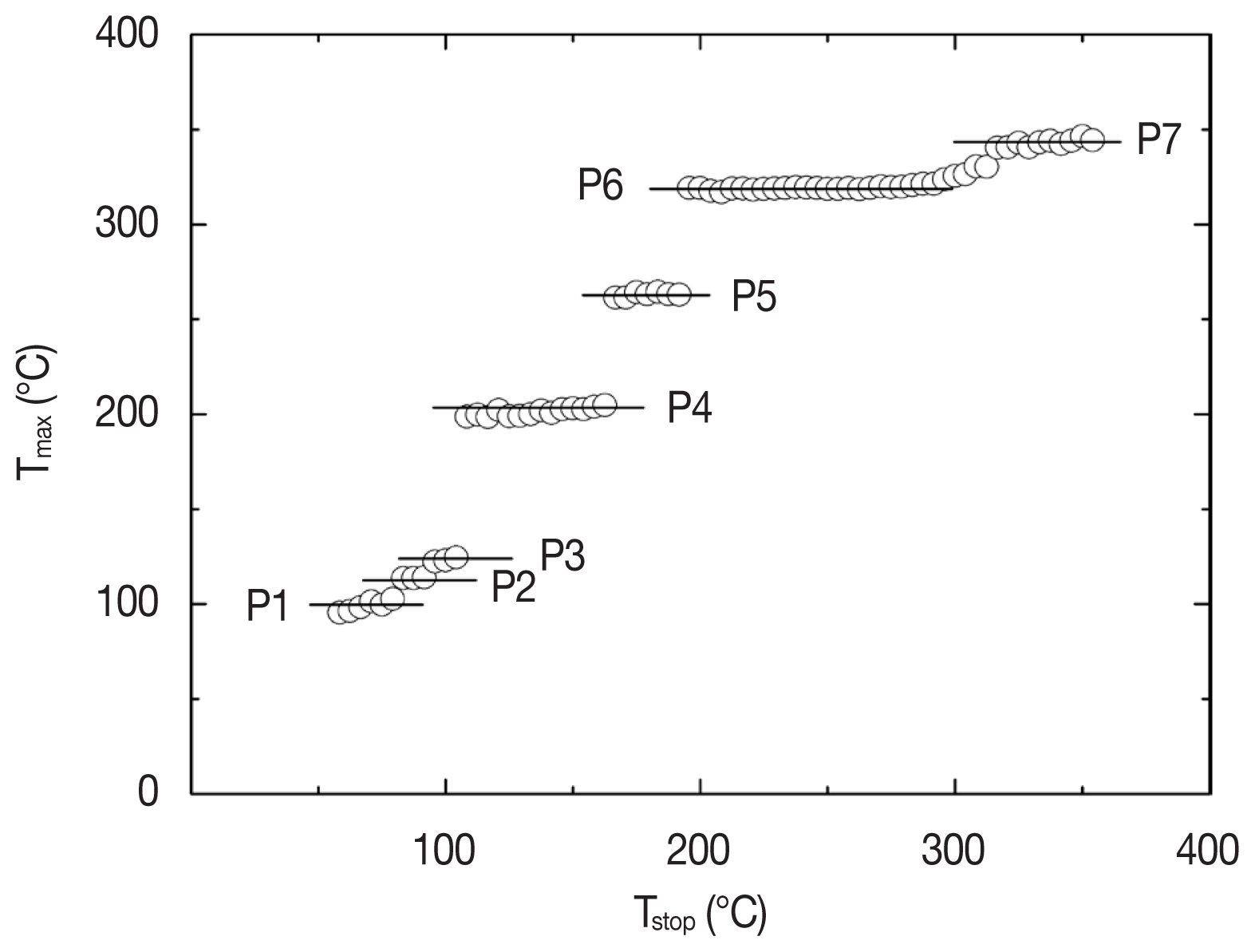
First maximum temperatures (Tm) of remaining TL glow peaks versus each initial heating temperature (Tstop).
With those information, we analysed the glow peaks to procure the trap parameters of the each peak using the CGCD method combined with the general order kinetics [12]. The general order kinetics used is expressed by
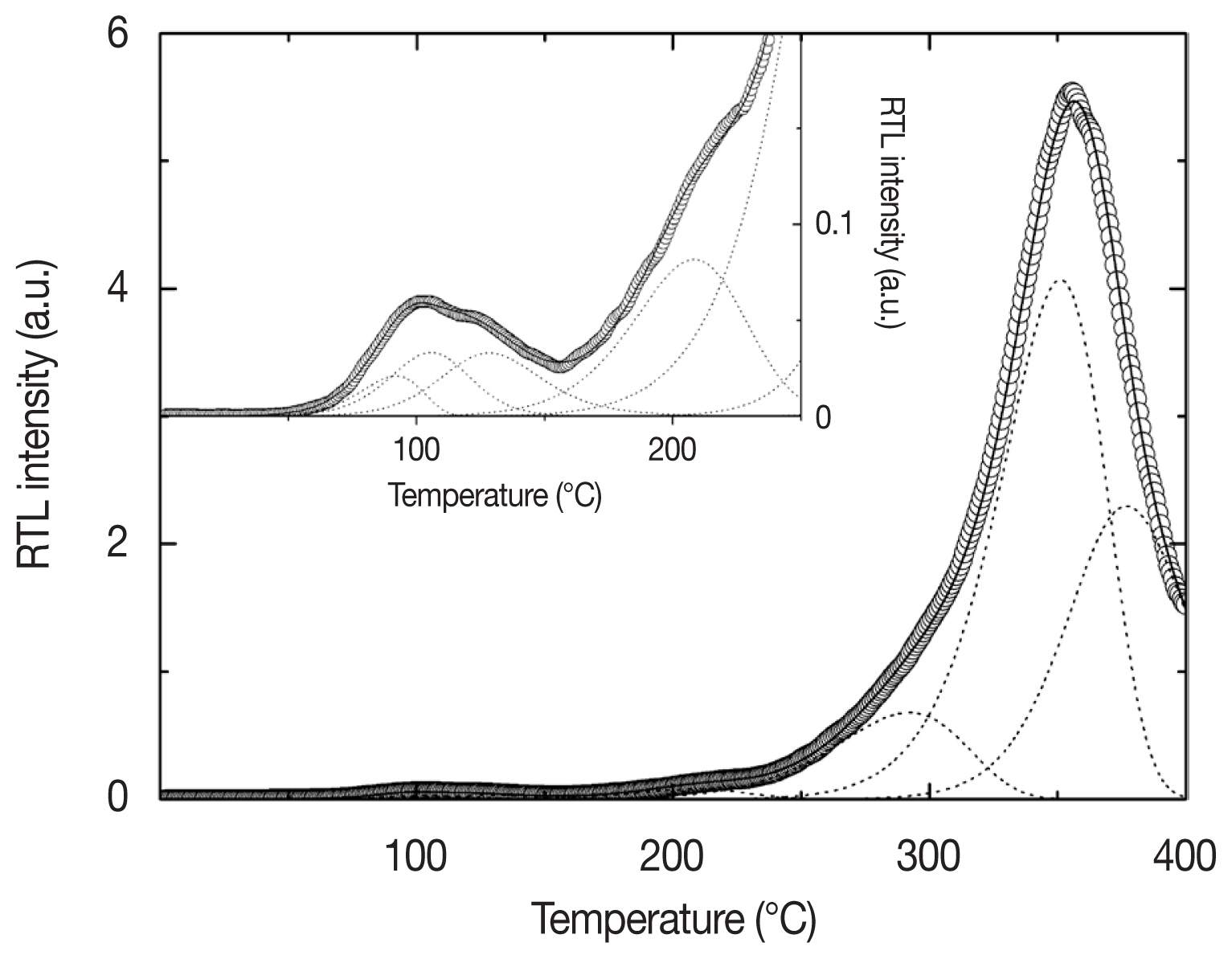
where Δ=2kbT/E, Δm=2kbTm/E, Zm=1+(b-1)Δm, I is the intensity of glow peak, E is the activation energy, kb is the Boltzmann constant, T is the absolute temperature and b is the order of the kinetics. In this approach, the values of E, T, and b were individually obtained by repeated fitting processes. The Mathematica software (version 9.0) was used for this analysis. Figure 5 shows the separated glow peaks after correcting the thermal quenching. The RTL glow curves were resolved into seven glow peaks centered at 92, 106, 128, 208, 292, 351, and 377°C, listed as P1–P7, respectively. The activation energies and the order of kinetics determined for individual peaks are represented in Table 1. The good-of-fit for the separated glow curves was tested by the figure of merit (FOM) [13]:

Activation Energies (E) and Order of Kinetics (b) of the RTL Quartz Determined after Correcting the Thermal Quenching
In this equation, Yi is the experimental value and fi is the best-fit value of the TL intensity. Balian and Eddy [13] recommend 2.5% to declare a fit as good. The FOM value obtained was 1.5%, which indicates that the fit is successful.
4. Optical sensitivity
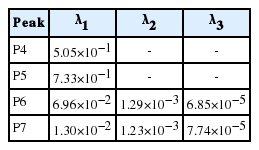
The optical sensitivity for the RTL quartz sample was examined by comparing the change of intensity on RTL glow peaks measured after exposure to light from a solar simulator (SOL-2: Honle, Martinsried, Germany) with various illumination times. According to the manufacturer’s specification the solar simulator used in the present work provides a power density 910 W·m−2 at the sample position and about 6.5 times the brightness compared with sunlight. Following experiments were carried out for this investigation. After exposure with a beta dose of 300 Gy, the RTL measurements of the quartz sample were made up to 450°C with the samples exposed to various times to light from a solar simulator, from a few minutes to 416 hours. With these glow curves, the thermal quenching was corrected and then peak separation using the CGCD method mentioned earlier was made. Variations of the luminescence efficacy between samples were normalized using the 120°C peak intensity after giving a second monitor beta dose. Three aliquots in each measurement were employed. In this work, the four peaks (P4–P7) are of interest in retrospective dosimetry because the three peaks (P1–P3) possess a short life time. As a result of the decay modes for exposure to light from a solar simulator, the signals for peaks P4 and P5 exhibited one exponential fall represented by the functional form of f(t)=a1e−λ1t, while three different exponential decays expressed the functional form of f(t)=a1e−λ1t+a2e−λ2t+a3e−λ3t were shown for the signals for peaks P6 and P7.
The decay modes of the peaks P4 and P5 are shown in Figure 6A. During an exposure to light of 416 hours, a rapid initial decaying occurred, showing an exponential fall with time with a decay constant of λ1=5.05×10−1 min−1 for the peak P4 and 7.33×10−1 min−1 for the peak P5. Figure 6B shows the decay modes of the peaks P6 and P7. There is a rapid initial decaying and the decaying keeps more slowly with two different decay shapes, showing exponential fall with time with three decay constants of λ1=6.96×10−2 min−1, λ2=1.29×10−3 min−1 and λ3=6.85×10−5 min−1 for the peak P6, and λ1=1.30× 10−2 min−1, λ2=1.23×10−3 min−1 and λ3=7.74×10−5 min−1 for the peak P7. The decay constants are calculated using least-squares fits on the plot of linear-log scale and are displayed in Table 2. The times taken to reduce the RTL signal to half of its initial value were 70 seconds for the peak P4, 54 seconds for the peak P5, 9,840 seconds for the peak P6 and 26,580 seconds for the peak P7, respectively. Scholefield and Prescott et al. [3] presented the optical sensitivity for RTL quartz that the peaks at 270°C and 305°C gave a high optical sensitivity while an insensitive optical property showed for the peak at 350°C. This result supports the outcomes produced from the present study.

Normalized RTL responses according to various exposure times to light from a solar simulator of peaks (A) P4 and P5, (B) P6 and P7.
Conclusion
We investigated on the optical sensitivity of TL peaks separated by the CGCD method for RTL quartz. Using the Tm-Tstop method, we found the glow peak of RTL quartz measured in a temperature up to 450°C was overlapped with seven glow peaks. In addition, the general order kinetics model was appropriate to separate glow peaks. The optical sensitivity according to the exposure time to light from solar stimulation of the RTL signal for the dosimetric peaks exhibited only one exponential decay component for peak P4 and P5 and three different exponential decay components for peak P6 and P7. The times taken to reduce the RTL signal to half of its initial value were 70 seconds for the peak P4, 54 seconds for the peak P5, 9,840 seconds for the peak P6 and 26,580 seconds for the peak P7, respectively. From this result, we conclude that the optical sensitivity of peaks P4 and P5 gives much higher than that of peaks P6 and P7.
Acknowledgements
This research was supported by 2016 Research Grant from Kangwon National University (No. 520160283) and Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (NRF-2017R1D1A1B03029608).