A Copper Shield for the Reduction of X-γ True Coincidence Summing in Gamma-ray Spectrometry

Article information

Abstract

Introduction

A high purity germanium (HPGe) detector has been widely used for gamma-ray spectrometry because of its good resolution and there have been commercial planar, coaxial or well types. It can be fabricated to achieve higher detection efficiency especially for low energy photons. In this case, it often has a thin dead-layer, which is induced by forming an electric contact on the surface of the germanium crystal, and a thin window of a material with low atomic number such as carbon composite or beryllium. However, this can increase the summing effects for radionuclides emitting X-rays or gamma-rays in sequence within the resolving time of the preamplifier of a detector. This phenomenon is well known in gamma-ray spectrometry as a true coincidence summing effect. It can cause “summing in”, in which the full-energy peak is added to, by the sum of incident photons with different energies, or “summing out”, in which the full-energy peak is summed with other incident photons and recorded in a channel corresponding to a higher energy [1, 2]. This effect can also make efficiency calibration or spectrum analysis more complicated, especially for true coincidence summing by X-rays and gamma-rays (hereafter referred to as ‘X-γ summing’).

The X-γ summing effect can be neglected by attenuating low energy X-rays in a detector’s window, and this can simplify gamma-ray energy spectrum analysis because only γ-γ summing is considered. Low energy X-rays can be effectively attenuated using low atomic number materials, and Cu has generally been used as the most internal shielding material in gamma-ray detector shields to attenuate X-rays. Therefore, Cu could be useful for reduction of the X-γ summing effect in gamma-ray measurements. The purpose of this study is to test the feasibility of a Cu shield as an X-ray filter to avoid the X-γ summing effect. In this paper, the characteristics of low-energy photons attenuated by Cu, and the results of experiments and Monte Carlo simulation on the applicability of a Cu shield to an n-type HPGe detector, are presented.

Materials and Methods

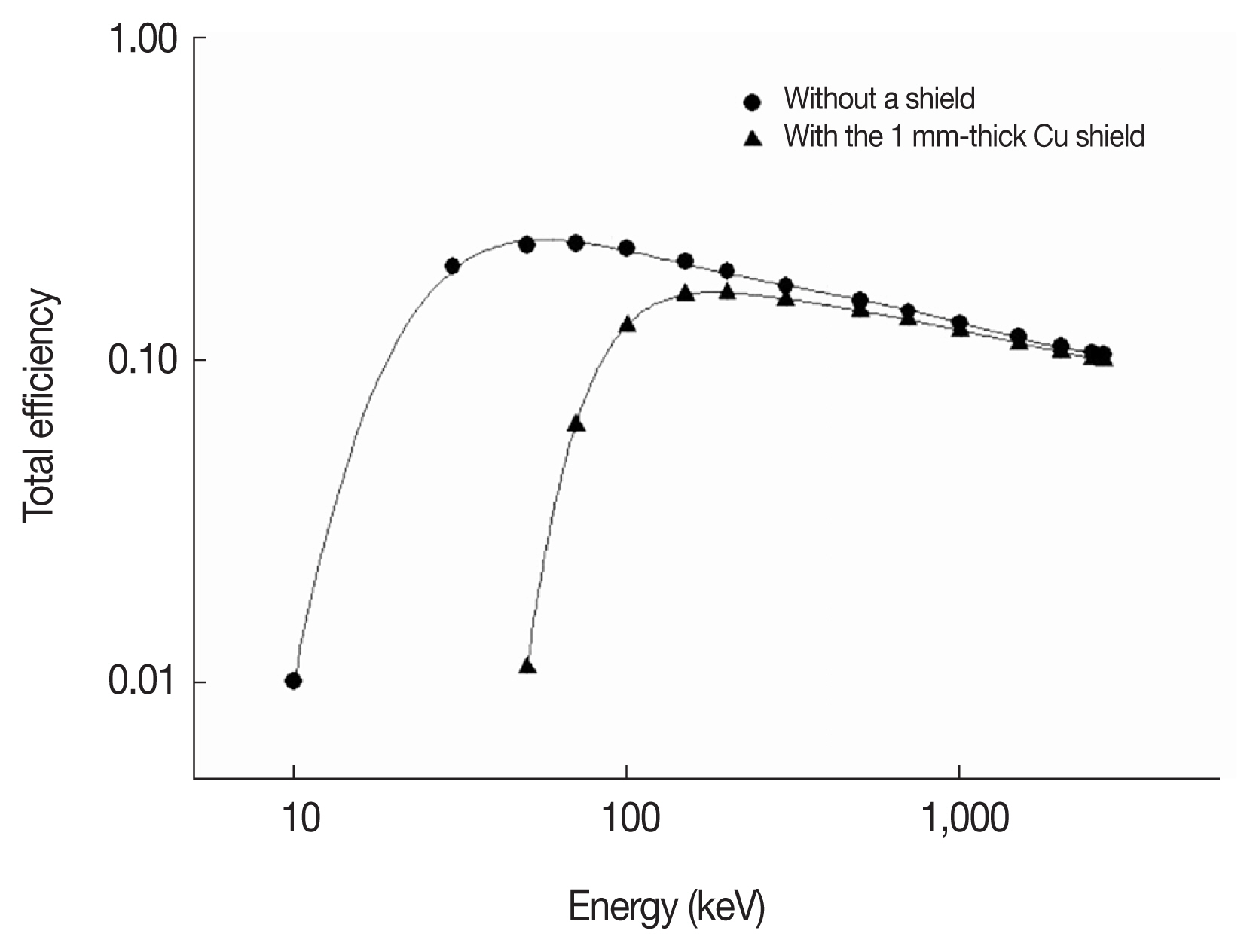
X-rays scattered in shielding materials surrounding a detector can be summed with gamma-rays in sequence within the resolving time of the detector. Therefore, in order to reduce effectively the X-γ summing by scattered X-rays, the X-rays from the gamma-ray source should be absorbed predominantly by photoelectric effects in the shielding materials. Figure 1A shows the ratio of photoelectric and total mass attenuation rates for Cu. The thickness of a Cu shield needs to be optimized considering the reduction rates of X-rays to produce the X-γ summing that minimizes the decrease of efficiency in the detection of gamma-ray energy. The linear attenuation rate of the energy lines of interest in Cu of varied thickness with XCOM^1),, was evaluated as shown in Figure 1B.

Fig. 1

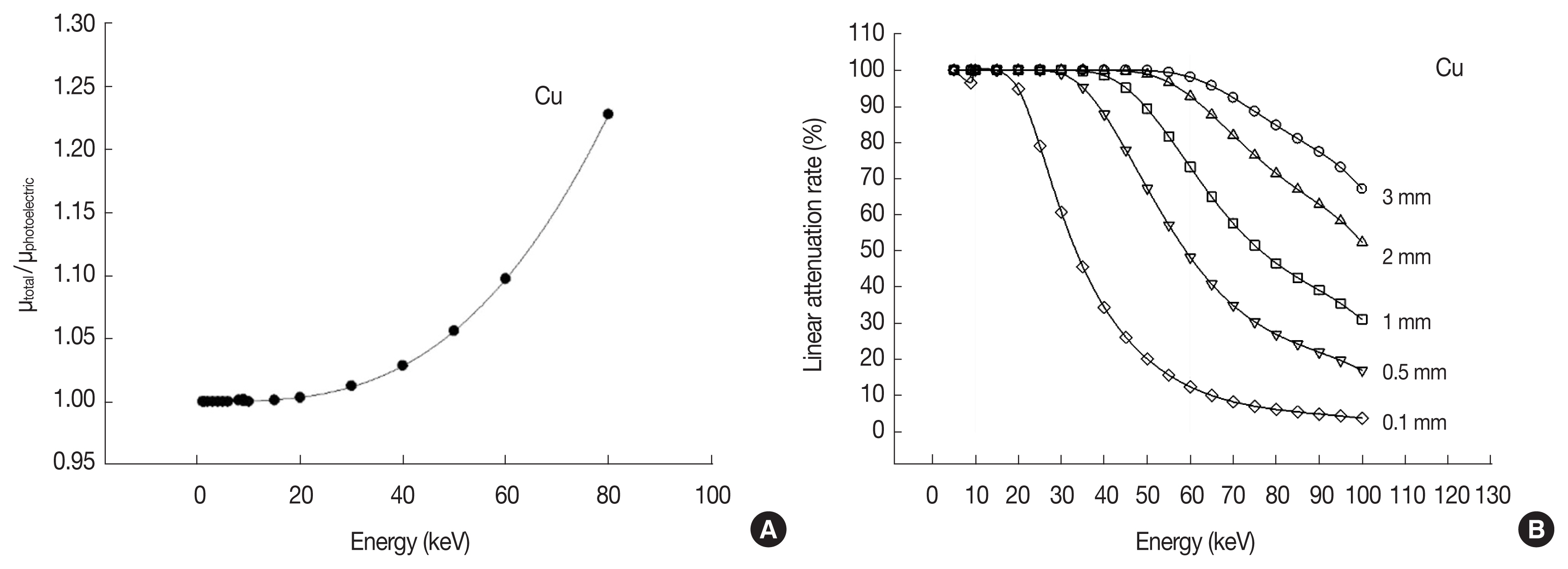
(A) Ratio of photoelectric and total mass attenuation rates and (B) photon linear attenuation rate excluding coherent scattering in Cu (ρ=8.96 g·cm⁻³).

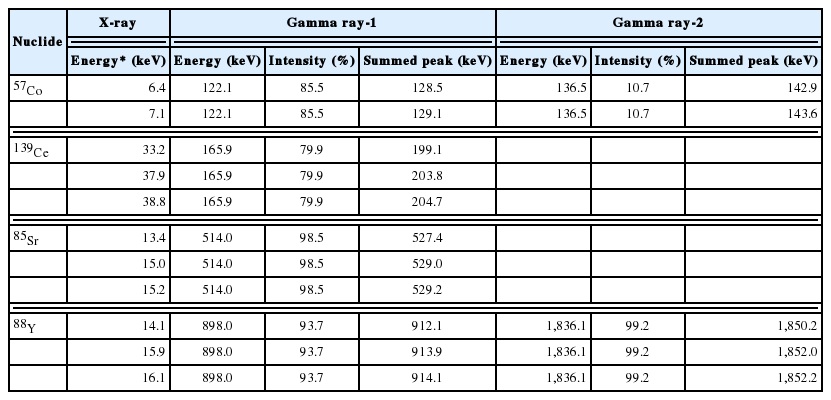
To estimate the feasibility of a Cu shield, one was applied to an HPGe detector to avoid the X-γ true coincidence summing effect during calibration of the absolute detection efficiency. An n-type coaxial HPGe detector with relative efficiency of 30% and commercial standard solution of mixed nuclides containing ²⁴¹Am, ¹⁰⁹Cd, ⁵⁷Co, ¹³⁹Ce, ¹¹³Sn, ²⁰³Hg, ⁸⁵Sr, ¹³⁷Cs, ⁶⁰Co, and ⁸⁸Y were used in this study. The standard source was diluted with 1 M HCl and filled with a layer 10 mm thick in a cylindrical bottle (4.8Ø×5 cm³); then measured using the HPGe detector. The radionuclides of ¹³⁹Ce, ⁸⁵Sr, and ⁸⁸Y in the source can significantly produce X-γ summing in gamma-ray spectrometers when using detectors with higher detection efficiency for low energy photons. This includes devices such as the n-type HPGe detector with a very thin dead layer.

Table 1 shows the range of the main gamma-ray energies to be produced by X-γ summing for the n-type HPGe detector with the commercial calibration source. It should be nearly attenuated to 40 keV X-ray from ¹³⁹Ce to avoid the X-γ summing effect during gamma-ray spectrometry. As shown in Figure 1B, the photon’s total linear attenuation rate for about 40 keV is nearly 99% in 1 mm-thick Cu with the general density of 8.96 g·cm⁻³. To minimize the decrease in detection efficiency, the optimal thickness was determined to be 1 mm. A Cu shield was made and attached to the bottom of a cylindrical sample holder for practical use, as shown in Figure 2.

Table 1

Main Gamma Ray Energy Peaks Produced by X-γ Summing in the Standard Mixed Gamma Source

Fig. 2

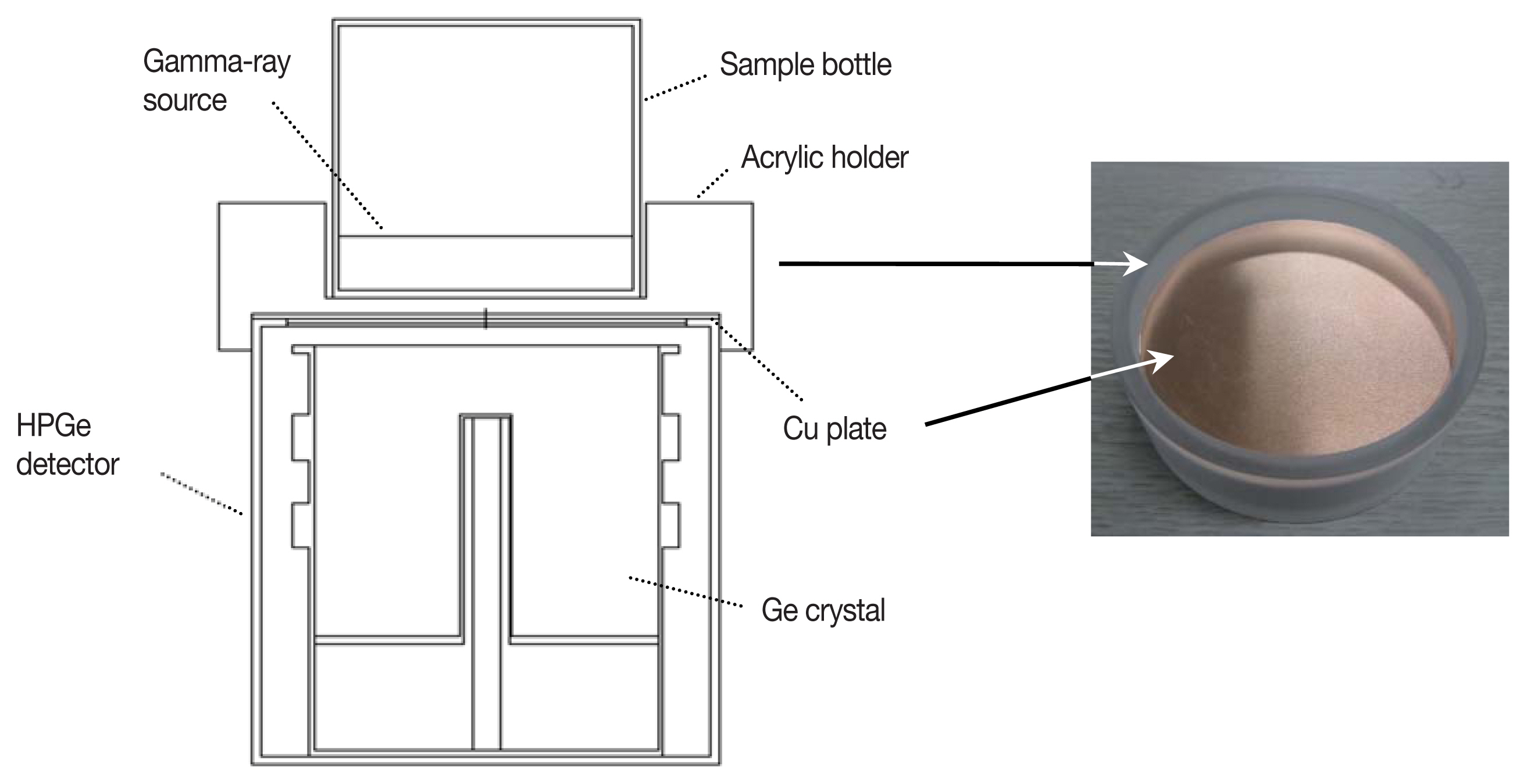
Geometrical model of the n-type HPGe detector system with a 1 mm-thick Cu shield using the MCNPX code.

The efficiency curves were compared for cylindrical standard sources 10 mm thick, with and without the Cu shield. The detection efficiency without X-γ summing effects was simulated to confirm the effectiveness of the Cu shield comparing with measured efficiency. To simulate the detection efficiency without γ-γ summing effects, a Monte Carlo simulation using the MCNPX code was conducted; the geometrical model is shown in Figure 2 [3–5]. The pulse height tally ‘F8:P’ with default physics option in the code was used to simulate the detection efficiency for the detector. The simulation was validated by comparing the measured and simulated results for ²⁴¹Am, ¹⁰⁹Cd, ²⁰³Hg, and ¹³⁷Cs contained in the standard source because the true coincidence summing can be neglected for the nuclides with the detector and gamma source used in this study. The true coincidence summing correction factors with and without the Cu shield were also calculated for ⁵⁷Co, ¹³⁹Ce, ⁸⁵Sr, ⁶⁰Co, and ⁸⁸Y in order to double-check the summing effect. The general formula for the factor (CF) can be expressed as

where

The internal conversion coefficients, electron capture probability and K-shell X-ray fluorescence needed for f_i were referenced the nuclear data from the Recommended Data (LNHB)²⁾, and ɛ_ti was obtained by the Monte Caro simulation in the same way mentioned above.

Results and Discussion

Figure 3 shows gamma-ray energy spectra with and without the 1 mm-thick Cu shield, and the X-γ summing peaks for ¹³⁹Ce, ⁸⁵Sr and ⁸⁸Y measured with the shield are not observed in the spectra because of X-ray filtering in contrast to ones without a shield. Figure 4 and Table 2 represent the measured and simulated detection efficiencies of the cylindrical source (4.8Ø×1 cm³) with and without, respectively, true coincidence summing. The absolute efficiencies for the full-energy peaks by measurement and simulation with and without the Cu shield for ²⁴¹Am, ¹⁰⁹Cd, ²⁰³Hg, and ¹³⁷Cs agreed well (within 3%). Figure 5 shows the simulated total efficiency, and there was good agreement between the calculated correction factor (CF) and the ratio of measured and simulated efficiency within 3%. This shows that the validity of the simulation was demonstrated. For the measurement system without a Cu shield, differences between the measured and simulated efficiencies for ¹³⁹Ce, ⁸⁵Sr, and ⁸⁸Y were larger than for other nuclides because of X-γ summing. The greatest difference was for ⁸⁸Y due to X-γ summing and γ-γ summing. In contrast, ²⁴¹Am, ¹⁰⁹Cd, ⁵⁷Co, ²⁰³Hg, ¹¹³Sn, and ¹³⁷Cs had small differences compared to ¹³⁹Ce, ⁸⁵Sr, and ⁸⁸Y because the true coincidence summing for the nuclides can be neglected in the spectrometer used in this study. The X-γ summing for ⁵⁷Co with the present volume source can be neglected, but it can be occurred significantly for a point source or thin paper filter source close to the detector which has high detection efficiency for low energy. The measured efficiencies with the Cu shield agreed with the simulated ones within 3% except for ⁸⁸Y and ⁶⁰Co. Due to γ-γ summing, ⁸⁸Y and ⁶⁰Co had larger differences than the other nuclides. The results show that the X-γ summing effect can be avoided using a Cu shield of appropriate thickness, and that the accuracy of the detection efficiency calibration for gamma-ray detectors with windows of thin or low atomic materials can be improved.

Fig. 3

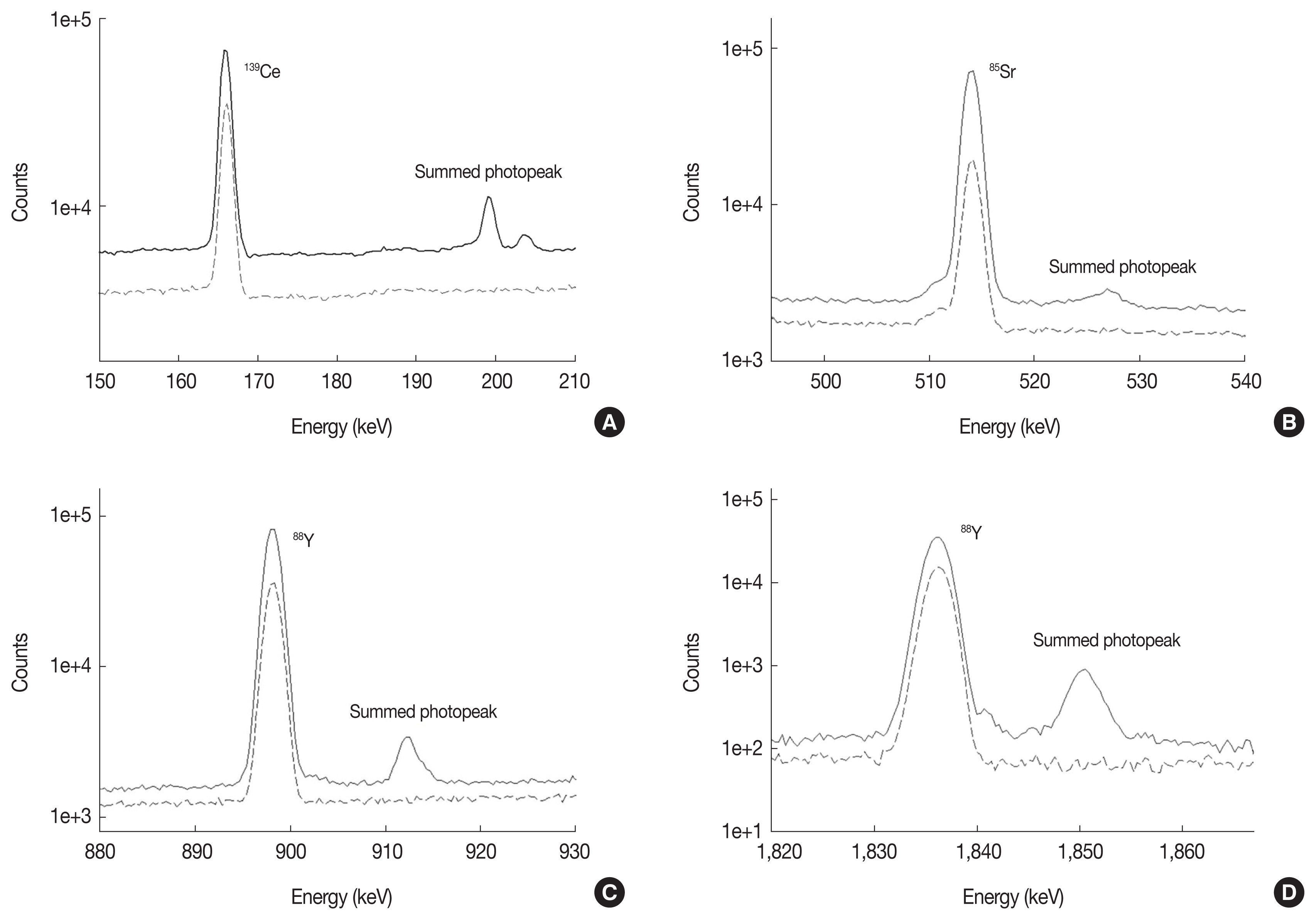
Pulse-height spectra obtained for a calibration source with (---) and without (—) the 1 mm-thick Cu shield.

Fig. 4

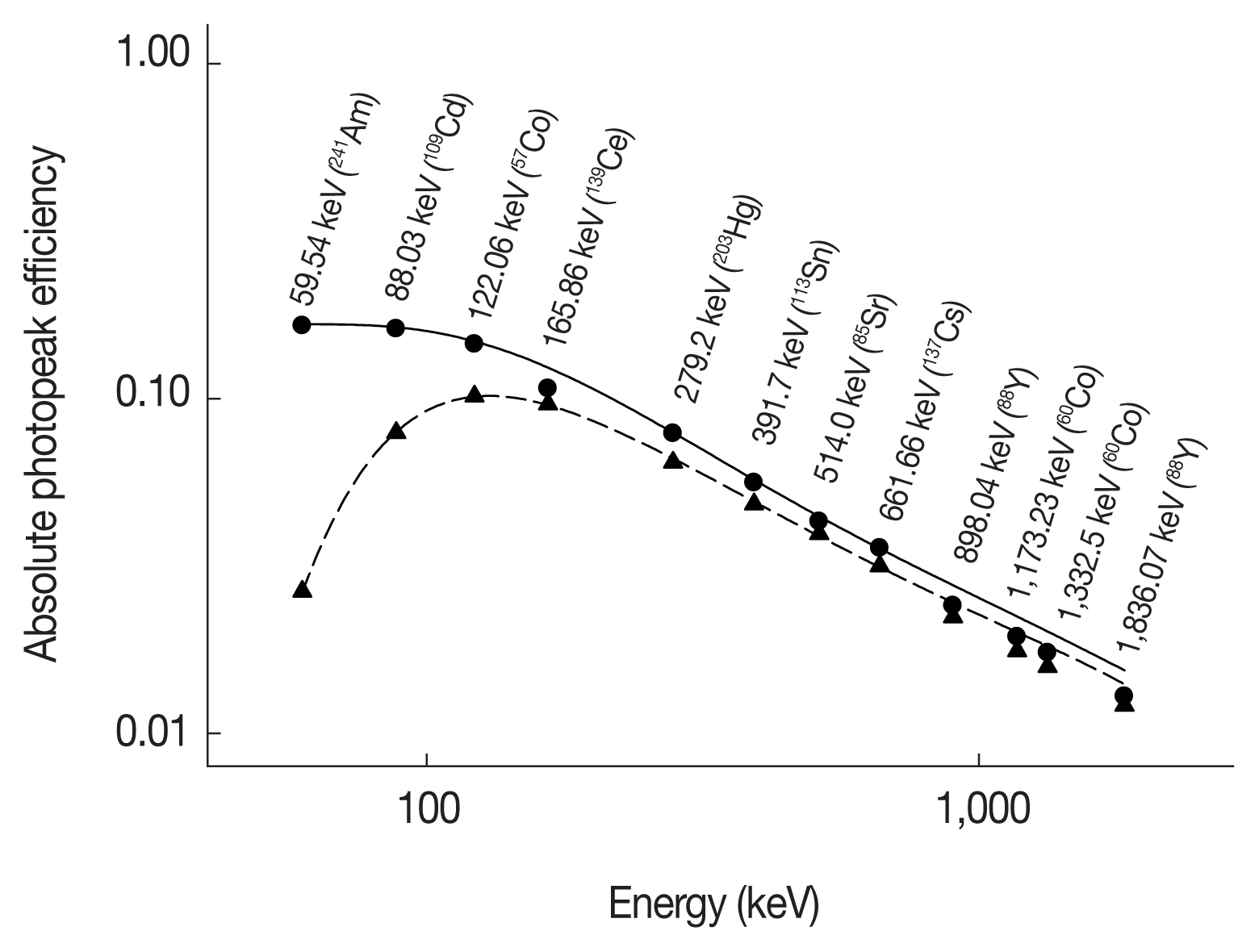
Detection efficiencies measured and simulated for the n-type HPGe detector systems with and without the 1 mm-thick Cu shield: (●) measured without a shield, (—) simulated and 6th-order fitted curve without a shield, (▲) measured with the 1 mm-thick Cu shield, (---) simulated and 6th-order fitted curve with the 1 mm-thick Cu shield.

Table 2

Measured and Simulated Detection Efficiencies for the n-type HPGe Detector System with and without the 1 mm-thick Cu Shield

Fig. 5

Total efficiency of an n-type HPGe detector for a liquid volume source (4.8Ø×1 cm³) with and without the 1 mm-thick Cu shield.

Conclusion

In this study, the thickness of a Cu shield needed to avoid true coincidence summing effects due to X-γ was tested and determined to be 1 mm, considering the detection efficiency desired for higher energy. As a result, the accuracy of the detection efficiency calibration was improved by more than 13% by reducing X-γ summing. Although gamma-ray detectors with a window consisting of thin or low atomic number materials (such as an n-type HPGe detector) are used for lower energy gamma-ray measurements, the use of appropriate shields can improve the applicability and accuracy of such detectors for high energy gamma-rays. The X-γ summing effect should be considered, along with γ-γ summing, when a detection efficiency calibration is implemented. This is particularly true for gamma-ray detectors having photon incidence windows with thick or low atomic number materials. In such cases, appropriate shielding material such as Cu can be useful for simplifying analysis of the gamma-ray energy spectrum during detection-efficiency calibration and for improving the quantification of radioactivity in test samples by avoiding X-γ summing effects.

Article information Continued