AbstractBackgroundFour-dimensional computed tomographic (4DCT) images are increasingly used in clinic with the growing need to account for the respiratory motion of the patient during radiation treatment. One of the reason s that makes the dose evaluation using 4DCT inaccurate is a change of the patient respiration during the treatment session, i.e., intrafractional uncertainty. Especially, when the amplitude of the patient respiration is greater than the respiration range during the 4DCT acquisition, such an organ motion from the larger respiration is difficult to be represented with the 4DCT. In this paper, the method to generate images expecting the organ motion from a respiration with extended amplitude was proposed and examined.
Materials and MethodsWe propose a method to generate extra-phase images from a given set of the 4DCT images using deformable image registration (DIR) and linear extrapolation. Deformation vector fields (DVF) are calculated from the given set of images, then extrapolated according to respiratory surrogate. The extra-phase images are generated by applying the extrapolated DVFs to the existing 4DCT images. The proposed method was tested with the 4DCT of a physical 4D phantom.
Results and DiscussionThe tumor position in the generated extra-phase image was in a good agreement with that in the gold-standard image which is separately acquired, using the same 4DCT machine, with a larger range of respiration. It was also found that we can generate the best quality extra-phase image by using the maximum inhalation phase (T0) and maximum exhalation phase (T50) images for extrapolation.
ConclusionIn the present study, a method to construct extra-phase images that represent expanded respiratory motion of the patient has been proposed and tested. The movement of organs from a larger respiration amplitude can be predicted by the proposed method. We believe the method may be utilized for realistic simulation of radiation therapy.
IntroductionPatient quality assurance (QA), assessment of dose delivered to the patient, is a procedure to evaluate a radiation treatment. With increasing complexity of treatment planning and delivery, the QA procedure is also evolved for proper evaluation of advanced radiation treatment [1]. Historically, dosimetric QA have been conducted by measuring point or plane dose with simple phantom [2]. It is then conducted in a patient-specific way by involving a patient anatomy with a radiological image [3ŌĆō5]. The patient QA is now growing to assess the patient dose more realistically, by reflecting many factors of actual treatment (e.g., beam log, organ motion). By reconstructing a volumetric dose distribution, the patient-specific QA is expected to offer more intuitive and clinically meaningful information to the physician and the physicist.
Another issue with growing interest as radiation therapy technique advances is the intrafraction motion. Among many reasons that cause intrafraction motion, respiratory motion is the topic that the most research studies and developments are focused on. Since respiratory motion shows no general pattern, as many published studies mentioned [6], the patientsŌĆÖ unique motion should be accounted individually. Hence, the patient image with respiratory movement, such as 4-dimensional computed tomographic (4DCT) image, is commonly utilized to consider the respiratory motion [7ŌĆō9].
Recently, there have been a number of studies involving respiratory motion on dose calculation for patient QA of the radiation treatment using 4DCT. Dowell et al. [10] and Paganetti et al. [11] proposed a time dependent geometry simulation, using deformable image registration [12, 13] on the patientŌĆÖs 4DCT data to account for organ movement and generate composite dose in Monte Carlo simulation. Han et al. [14] proposed an advanced 4D voxel phantom that deforms continuously, by generating many additional phases between existing phases of 4DCT using DIR and linear-interpolated DVFs. The continuity of the movement in that phantom enables accurate evaluation of inter-play effect.
In those studies, that utilize 4DCT to reflect respiratory motion in dose calculations, the respiration of the patient is assumed to be stable and regular. However, the respiration of the patient is not always maintained in a such stable state, but may change during the therapy session [15]. Since the 4DCT only contains the images of the patient anatomy only within a certain respiratory range from which the 4DCT was acquired, the patientŌĆÖs anatomy cannot be accounted on dose calculation with the 4DCT if the patientŌĆÖs respiration deviates from the respiratory range of 4DCT acquisition (i.e., greater degree of inhalation or exhalation). Such absence of the patient image outside of the respiratory range has not been concerned on the studies using 4DCT for dose calculation. The discordance between the actual patient anatomy and the images used for dose calculation may cause error on dose distribution. Proper evaluation of respiratory movement to 4D patient dose of radiation therapy would require, we believe, adequate reflection of such irregularity on respiratory amplitude of the patient during the session.
To address this limitation, in the present study, we proposed a method to account for the organ motion from the greater respiratory amplitude than the range of 4DCT acquisition by generating images that represent patient anatomy of corresponding respiratory amplitude. We named such images ŌĆ£extra-phase imagesŌĆØ as they supplement 4DCT images like additional respiratory phases, so that they enable one to account for the organ motion of extended range of respiration amplitude.
To generate the extra-phase image, a motion model, accounting for an inter-cycle variation, was formed based on 4DCT. Deformable image registration (DIR) is used to calculate the deformation of images for each phases of respiratory cycle. The calculated deformation vector field (DVF) is then correlated to a single surrogate signal with a linear correspondence model. The linear model was adopted since it is less susceptible to extrapolation errors than polynomial models [16]. The model is applied to generate the extra-phase image, with respect to the respiration amplitude measured by external surrogate. The extra-phase images, generated with accordance to patientŌĆÖs actual respiration, would be applied to a simulation of radiation treatment, so that the effect of irregularity on the respiratory amplitude can be reflected in a dose calculation. The calculated dose can be utilized in various ways, such as treatment evaluation, plan verification, and adaptive therapy.
The proposed method was examined for verification and optimization by applying it on 4DCT images of a physical phantom with various configurations. The extra-phase images for larger respiratory amplitude were generated from the 4DCT images of the phantom with a smaller respiration. Then the generated images were compared with images that were actually acquired at a larger respiration.
Materials and Methods1. Extra-phase image generation methodIn this research, there are two assumptions for constructing a motion model to generate extra-phase image. The first assumption is that the organ movement is consistent. The direction and velocity of the movement would change gradually not abruptly. Then the movements of organs toward deep breath can be substituted by extension of the movement appeared in the existing 4DCT. The second assumption is that the magnitude of the organ movement is proportional to the amplitude of an external respiratory surrogate [17]. Then an extrapolation ratio can be deduced from patientŌĆÖs respiratory surrogate signal. With these two assumptions, we proposed a method to generate an extra-phase image with the following three steps: (i) calculation of organ motion in the 4DCT, (ii) extrapolation of the motion vector, and (iii) deformation of image with extrapolated vector. The procedure of extra-phase image generation is illustrated in Figure 1, and its detailed descriptions is given in the rest part of this section.
When applying DIR on the 4DCT images to generate an artificial image, we refer to the DIR with respect to reference phase (DRP) method, described in the paper of Han et al. [14]. Their method, generating additional images between existing phases with respect to a reference phase image rather than a neighboring phase image, shows less error in dose calculation that use the images as a Monte Carlo simulation geometry. We adopted this method to generate extra-phase images with consideration of future work, utilizing the extra-phase images for a dose calculation.
The first step is calculating motion among the existing 4DCT images. Two phase images, a fixed image and a moving image, are selected for applying DIR. Then, the movement of the organ between the two images is calculated as DVFmovingŌåÆfixed, or simply DVFmoving since the fixed image is set to be a reference phase image, T50. In order to generate an extra-phase image with respect to the fixed image, the inverse DVFmoving (i.e., iDVFmoving) is used in this research.
Then, the iDVF is extended based on the respiratory signal, which is measured by external surrogate device. Linear extrapolation is applied to the iDVF with a factor R, a ratio of the respiration displacement where extra-phase image is generated (i.e., between fixed image and extra-phase image to be generated) and where DVF is calculated (i.e., between moving image and fixed image).
Finally, the extrapolated iDVF is applied to deform the fixed image. Each voxel on the fixed image is warped according to the extrapolated iDVF, and the image intensity of the voxels are recalculated. Then the extra-phase image that represents the patient anatomy at greater respiration is generated.
2. Physical phantom configurationThe deformable moving lung phantom (DML phantom) [20] was used for assessment of the proposed method. As displayed in Figure 2, it consists of a balloon filled with a damped sponge to substitute a lung, mounted in a Lucite cylinder. A plastic sphere is placed inside of the lung, representing a tumor. The respiratory motion is simulated by a programmable motor-driven piston according to an arbitrary breathing profile.
We acquired sets of 4DCT images of the phantom with different tumor sizes and positions, 8 cases in total. We used the tumor size of 2, 3, 5 cm in accordance with the upper size limit of lung cancer staging criteria [21] of T1a, T1b and T2a, respectively. The tumor was placed at three different positions (top, middle and bottom), dividing the lung into quarters. In case of the tumor with 5 cm size, it was too bulky to put it on the top position, so only the middle and the bottom positions were investigated.
For each case, two sets of 4DCT were acquired while the phantom was driven in a sinusoidal wave with two respiratory amplitudes of 10 mm and 20 mm; the amplitude of 10 mm stands for the regular respiration during 4DCT scan, and 20 mm stands for a larger respiration. The 4DCT from the larger respiration is used as a gold-standard to evaluate the accuracy of the generated extra-phase image.
The 4DCT images were acquired using a Siemens SOMATOM Definition AS CT scanner (Siemens, Erlangen, Germany). Each set of the 4DCT is composed of 10 phases of respiratory-sorted 3D images with 512├Ś512├Ś97 of voxel resolution and 0.6348├Ś0.6348├Ś2 mm3 of voxel size. A Real-time Position ManagementŌäó (Varian Medical Systems, Palo Alto, CA, USA) was used to measure the respiratory signal of the phantom.
3. Performance evaluation and optimizationTo evaluate the performance of the propose method, we generated extra-phase images that correspond to maximum exhalation of 20 mm respiratory amplitude, with 4DCT acquired in 10 mm respiratory amplitude. Then the generated extra-phase images were assessed by comparing them to gold-standard images, which are actual images acquired with the 20 mm of respiratory amplitude. The corresponding images were examined visually and the tumor position on each image was compared. In addition, the Hounsfield unit (HU) difference between two images was inspected, within the region of interest (ROI) set around the tumor in the phantom image.
To deduce the optimal phase to derive iDVF, 5 iDVFs were calculated with the moving image of T0 (starting exhalation), T10, T20, T30, and T40 respectively. Each iDVFs was extrapolated with corresponding respiration ratio, and applied for deforming the reference phase image, T50. The extra-phase images generated with different iDVFs were examined by comparing them with the gold-standard image.
Results and Discussion1. Verification of extra-phase image generation methodThe generated extra-phase image for the case with the tumor size of 3 cm at the bottom position is illustrated with the existing images and the gold-standard image in Figure 3. To generate the extra-phase image, iDVFT0 was used which was calculated by using the maximum inhalation image, T0, as a moving image (Figure 3A) and the maximum exhalation image, T50, as a fixed image (Figure 3B). The range of motion of the tumor, which can be seen from the existing 4DCT with the 10 mm amplitude, Figure 3A and 3B, shows a large difference from the tumor position at the gold-standard image (Figure 3D), ranging from 5 mm to 13 mm. On the other hand, as can be seen in Figure 3C, the tumor position on the extra-phase image was in a good agreement with the tumor position on the gold-standard image. The difference of the tumor position between the extra-phase image and gold standard image was about 2 mm, which is acceptable considering the slice thickness of the CT image is 2 mm.
2. Optimization of iDVF generationThe iDVFs to generate extra-phase images were calculated with different moving images, T0ŌĆōT40, and each of them was used to generate an extra-phase image. Between extra-phase images and gold-standard image, the differences of the image intensity within the ROI are illustrated as subtraction images in Figure 4 for each of iDVFs used in extrapolation. The area with high HU difference, shown in white, was observed the least in Figure 4A, the extra-phase image generated with iDVFT0. This area is increased as the phase of the moving image approaches the phase of the fixed image (Figure 4BŌĆō4E).
A similar trend was found in the histogram analysis. Figure 5 illustrates the histograms which show the percentage of pixels as a function of HU difference within the ROI for different iDVF. The maximum difference of 1,175 was observed when the T50 image, the image before applying the proposed method, was compared to the gold-standard image. It was decreased to 660 when the T0 image is used as the moving image to generate the iDVF.
The results from all 8 cases with different tumor size and positions are illustrated in a box plot in Figure 6 which considers only the pixels with HU difference greater than 100. The proportion of pixels with high HU difference was ranged from 12.9% to 24% before applying the proposed method. Again, the smallest values are observed when the T0 image was used to generate the iDVF; the value was ranged from 3.6% to 7.3%, decreased by 67% on average when compared to those of images before applying the proposed method. Among the 8 cases with different tumor size and location, it is found that the proportion of pixels with high error was large when the tumor was located on the lower part of the phantom. This is because the magnitude is grater on the lower side of the phantom than upper side. On the other hand, there was little effect of the tumor size on the accuracy.
Our results show that the best performance is observed when the T0 image is used to calculate iDVF. This result is due to the fact that the organ motions stop at T0, the maximum inhalation phase, resulting in the best image quality with least motion artifact. In addition, the iDVF might be calculated precisely when using the T0 for the moving image, since T0 shows largest and clear movement from the fixed image, T50.
On the generated image, the tumor size was smaller compared to that of the gold-standard image, as shown in Figure 3C and 3D. One of the possible reason is registration error occurred during the calculation process of the DVF. On DIR calculation, entire volume of the image is assumed to be deformable, while on the phantom, only the lung part is deformable and the tumor is solid. Such discordance increases the registration error, and results in reduced tumor size on the generated image. Similar error was found from the results of different tumor size and position. The size difference was mainly occurred in SI direction and its magnitude about 2 mm, similar to the slice thickness, in all 8 cases. Such registration error is expected to affect the accuracy of the tumor positon estimation or the dose calculation. However, considering the difference of the tumor position between two respiratory amplitudes is much larger than the registration error, it is able to reduce an amount of potential error on the tumor position estimation and the dose calculation using the proposed method.
Note that because the geometry of the phantom is discretized into a certain size of voxels, some motion vectors which are smaller than, or comparable to, the voxel size can be ignored and, on the other hand, some motion vectors which are slightly larger than, or comparable to, the voxel size can contain a very large relative error. In addition, the extrapolation of such small vectors with a large extrapolation ratio can amplify the relative error. Hence, it is recommended to select the moving image for the calculation of iDVF that minimizes both the relative error in the iDVF and the extrapolation ratio. The T0 image as the moving image satisfies the requirement, as verified by the results of the present study.
The extra-phase image generation method proposed in the present study will be used to construct an advanced 4D computational phantom. When a patientŌĆÖs respiration become larger during the treatment session, the patientŌĆÖs anatomy and respiratory motion can be estimated by applying proposed method in accordance with a surrogate data. Since extra-phase images can be generated at any respiration positions, the patientŌĆÖs respiration with extended amplitude range can be represented as a series of them. Then, using generated extra-phase images as a computational phantom, a simulation geometry, along with a 4DCT, dose distribution that reflects actual patient respiration during treatment can be calculated. Such a phantom will be able to offer further information for patient QA.
The physical phantom used in the present study is designed to simulate a deformation motion of a lung. However, the motion and the inner structure are significantly simplified compared to those of the actual organ. The difference of complexity in the motion and the structure may affect the accuracy of the image registration. Hence, for clinical application, the extra-phase image generation method will be verified with the CT images of patients. Since patientsŌĆÖ organs show more complex structure, movement, and deformation, the valid range of motion that can be expected with the extra-phase image generation method is expected to be limited to some degree. In addition, it is possible to acquire two sets of 4DCT images of the phantom with different respiratory amplitude to verify the proposed method, but it may be difficult to acquire such images of patients with controlled respiratory amplitude, requiring thorough respiration training and guide.
ConclusionIn the present study, a method to construct extra-phase images from the existing 4DCT images using DIR and linear extrapolation was developed to consider extended respiratory motions. The developed method was then tested with the 4DCT images of a 4D physical phantom. The study suggests that the organ movement of a larger respiration amplitude can be predicted by extrapolating the DVF generated from the existing 4D images. The proposed method may find useful application in realistic simulation of radiation therapy, for better evaluation of patient dose.
AcknowledgementsThis research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2016R1D1A1A09916337), and by the Nuclear Safety Research and Development (NSR&D) Program through the Korea Foundation of Nuclear Safety (KoFONS) funded by Nuclear Safety and Security Commission (NSSC) (Project Number: 1705006).
References1. Feygelman V, Nelms B. Dosimetric quality assurance of highly conformal external beam treatments: from 2D phantom comparisons to 4D patient dose reconstruction. J Phys Conf Ser. 2013;444:012012.
2. Ezzell GA, et al. IMRT commissioning: Multiple institution planning and dosimetry comparisons, a report from AAPM Task Group 119. Med Phys. 2009;36(11):5359-5373.
3. van Elmpt W, Nijsten S, Mijnheer B, Dekker A, Lambin P. The next step in patient-specific QA: 3D dose verification of conformal and intensity-modulated RT based on EPID dosimetry and Monte Carlo dose calculations. Radiother Oncol. 2008;86(1):86-92.
4. Renner WD, Sarfaraz M, Earl MA, Yu CX. A dose delivery verification method for conventional and intensity-modulated radiation therapy using measured field fluence distributions. Med Phys. 2003;30(11):2996-3005.
5. van Elmpt W, Nijsten SM, Schiffeleers RF, Dekker AL, Mijnheer BJ, Lambin P, Minken AW. A Monte Carlo based three-dimensional dose reconstruction method derived from portal dose images. Med Phys. 2006;33(7):2426-2434.
6. Keall PJ, et al. The management of respiratory motion in radiation oncology report of AAPM Task Group 76. Med Phys. 2006;33(10):3874-3900.
7. Schreibmann E, Chen GT, Xing L. Image interpolation in 4D CT using a BSpline deformable registration model. Int J Radiat Oncol Biol Phys. 2006;64(5):1537-1350.
8. McClelland JR, Blackall JM, Tarte S, Chandler AC, Hughes S, Ahmad S, Landau DB, Hawkes DJ. A continuous 4D motion model from multiple respiratory cycles for use in lung radiotherapy. Med Phys. 2006;33(9):3348-3358.
9. Yang D, Lu W, Low DA, Deasy JO, Hope AJ, Naqa IE. 4D-CT motion estimation using deformable image registration and 5D respiratory motion modeling. Med Phys. 2008;35(10):4577-4590.
10. Dowdell S, Grassberger C, Sharp GC, Paganetti H. Interplay effects in proton scanning for lung: a 4D Monte Carlo study assessing the impact of tumor and beam delivery parameters. Phys Med Biol. 2013;58(12):4137-4156.
11. Paganetti H, Jiang H, Adams JA, Chen GT, Rietzel E. Monte Carlo simulations with time-dependent geometries to investigate effects of organ motion with high temporal resolution. Int J Radiat Oncol Biol Phys. 2004;60(3):942-950.
12. Chui H, Rangarajan A. A new point matching algorithm for non-rigid registration. Comput Vis Image Und. 2003;89(2):114-141.
13. Hualiang Z, Jeffrey VS. Monte Carlo dose mapping on deforming anatomy. Phys Med Biol. 2009;54(19):5815-5830.
14. Han MC, Seo JM, Lee SH, Kim CH, Yeom YS, Nguyen TT, Choi C, Kim S, Jeong JH, Sohn JW. Continuously deforming 4D voxel phantom for realistic representation of respiratory motion in Monte Carlo dose calculation. IEEE T Nucl Sci. 2016;63(6):2918-2924.
15. Foster KM, Stevens CW, Kitamura K, Chang JY, Cox JD, Guerrero TM, Jeter M, Liao Z, Starkschall G, Komaki R. Changes of tumor motion patterns during a course of radiation therapy for lung cancer, Int. J Radiat Oncol Biol Phys. 2003;57(2):S234.
16. McClelland JR, Hawkes DJ, Schaeffter T, King AP. Respiratory motion models: a review. Med Image Anal. 2013;17(1):19-42.
17. Gierga DP, Brewer J, Sharp GC, Betke M, Willett CG, Chen GT. The correlation between internal and external markers for abdominal tumors: implications for respiratory gating. Int J Radiat Oncol Biol Phys. 2005;62(4):1257.
18. Yang D, Brame S, El Naqa I, Aditya A, Wu Y, Goddu SM, Mutic S, Deasy JO, Low DA. Technical Note: DIRART - A software suite for deformable image registration and adaptive radiotherapy research. Med Phys. 2011;38(1):67-77.
19. Bruhn A, Weickert J, Schn├Črr C. Lucas/Kanade meets Horn/Schunck: combining local and global optic flow methods. International Journal of Computer Vision. 2005;61(3):211-231.
Fig.┬Ā1An illustration of the proposed extra-phase image generation method. The image generation method consists of 3 steps: (i) Calculation of organ motion as deformation vector field (DVF) from two images of 4DCT, moving image and fixed image. (ii) Extrapolation of DVF. Extrapolation ratio is decided according to the ratio of respiratory amplitudes. (iii) Deformation of fixed image using extrapolated DVF. 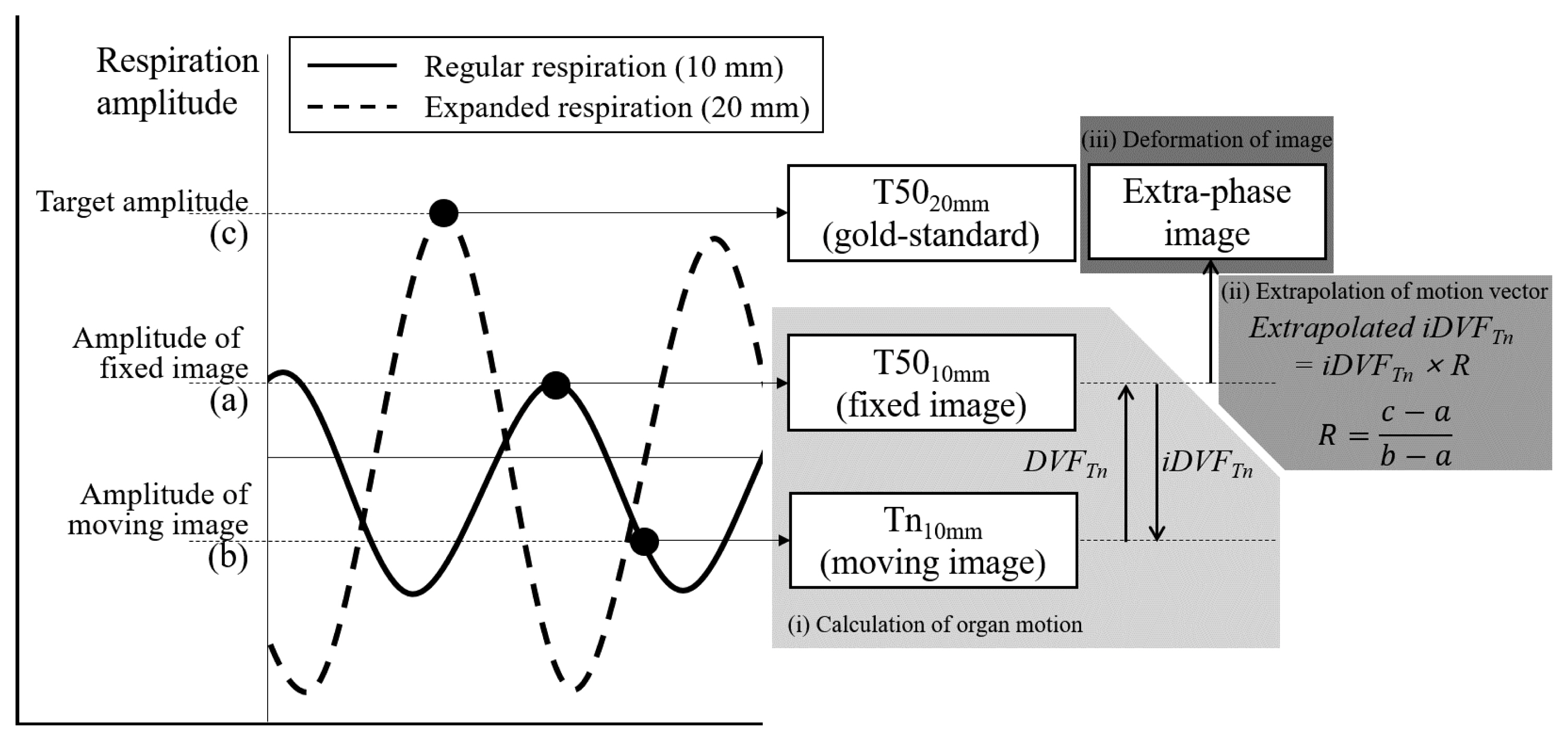
Fig.┬Ā3Coronal view of DML phantom CT image. (A) Maximum inhalation (T0) and (B) maximum exhalation phase (T50) of the 4DCT with 10 mm amplitude. (C) Extra-phase image generated from (A) and (B), to represent anatomy at deep exhale of 20 mm amplitude, (D) the gold-standard image, maximum exhalation phase of 20 mm amplitude. Yellow lines indicate tumor position of (D). 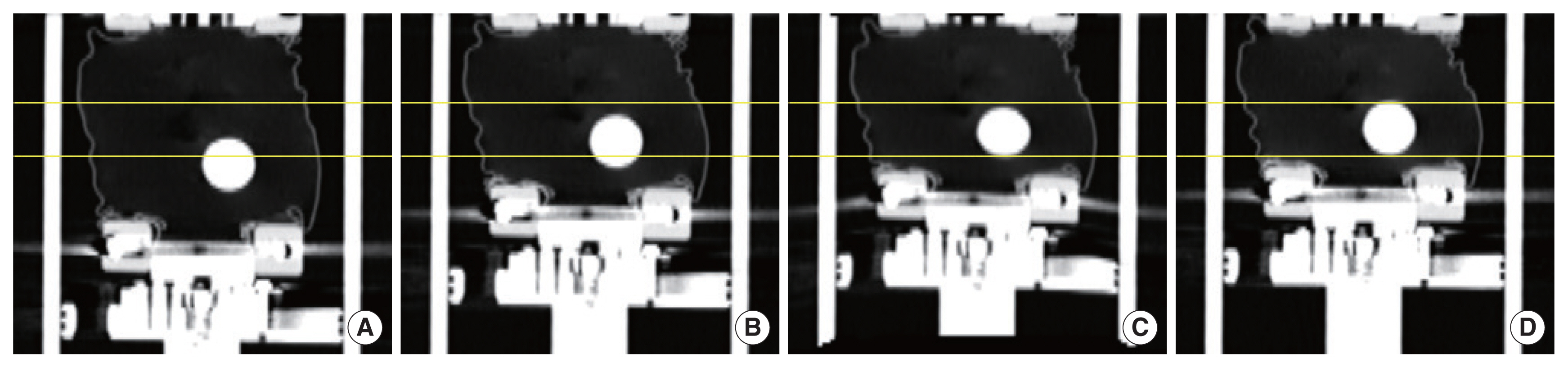
Fig.┬Ā4Coronal slice images showing the absolute difference between target images and gold standard image (T50 with 20 mm amplitude). (AŌĆōE) Target images are extra-phase image generated using T0ŌĆōT40 as moving image, respectively. (F) Target image is T50 of 4DCT with 10 mm amplitude, shown for comparison. 
Fig.┬Ā5Histogram of Hounsfield unit differences between gold standard image and extra-phase images generated with different moving image, within ROI. Compared to T50 with 10 mm amplitude, the generated images showed less difference. 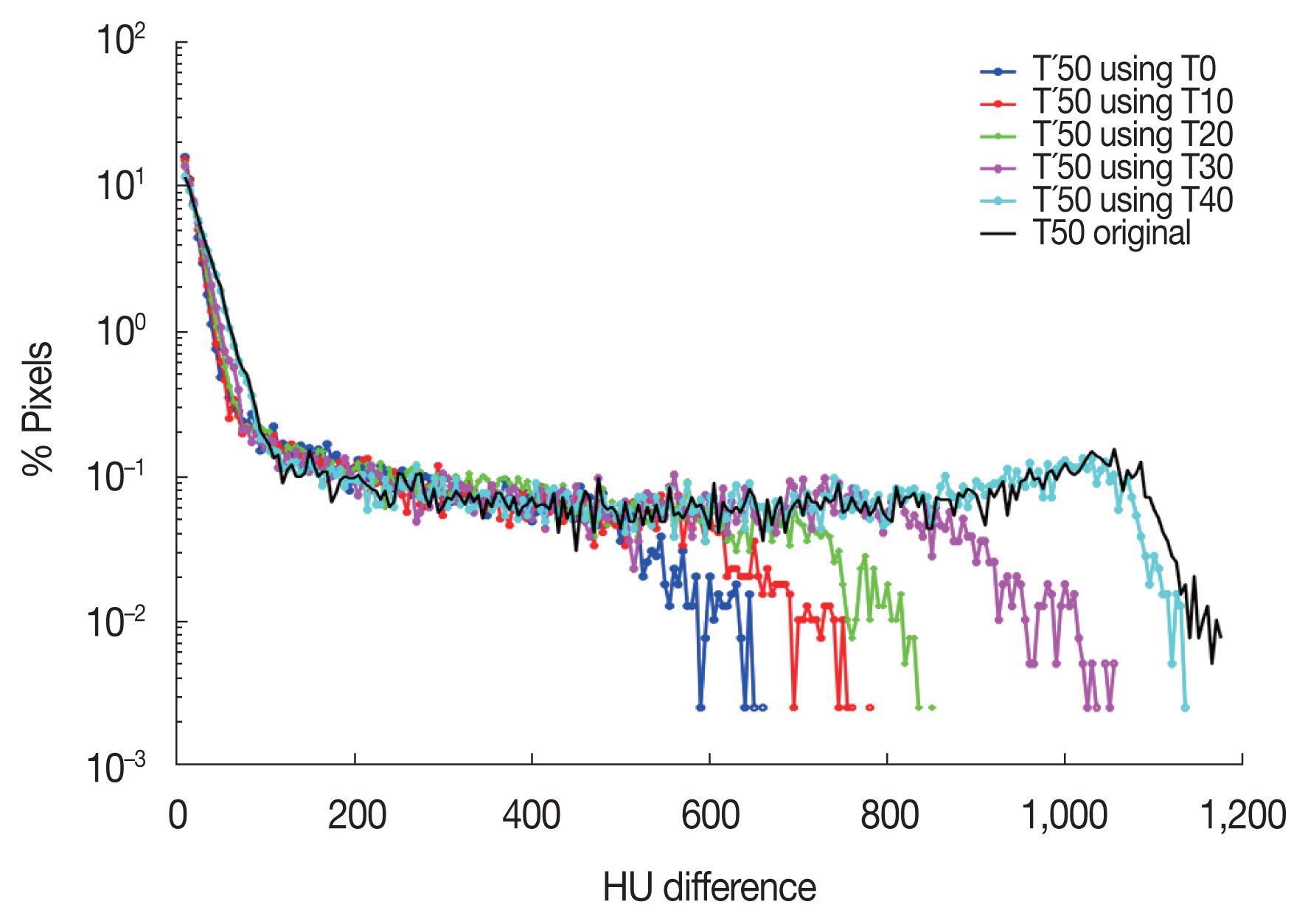
Fig.┬Ā6Box plot of the fractional voxel with Hounsfield unit difference more than 100 in all 8 cases. The boxes show the first quartile and the third quartile and red lines indicate median of the data. The extra-phase image generated using T0 as a moving image shows best agreement among 5 conditions. 
|
|
||||||||||||||||||||||||||||||||||||||||