AbstractBackgroundA gamma energy identifying algorithm using spectral decomposition combined with smoothing method was suggested to confirm the existence of the artificial radio isotopes. The algorithm is composed by original pattern recognition method and smoothing method to enhance the performance to identify gamma energy of radiation sensors that have low energy resolution.
Materials and MethodsThe gamma energy identifying algorithm for the compact radiation sensor is a three-step of refinement process. Firstly, the magnitude set is calculated by the original spectral decomposition. Secondly, the magnitude of modeling error in the magnitude set is reduced by the smoothing method. Thirdly, the expected gamma energy is finally decided based on the enhanced magnitude set as a result of the spectral decomposition with the smoothing method. The algorithm was optimized for the designed radiation sensor composed of a CsI (Tl) scintillator and a silicon pin diode.
Results and DiscussionThe two performance parameters used to estimate the algorithm are the accuracy of expected gamma energy and the number of repeated calculations. The original gamma energy was accurately identified with the single energy of gamma radiation by adapting this modeling error reduction method. Also the average error decreased by half with the multi energies of gamma radiation in comparison to the original spectral decomposition. In addition, the number of repeated calculations also decreased by half even in low fluence conditions under 104 (/0.09 cm2 of the scintillator surface).
ConclusionThrough the development of this algorithm, we have confirmed the possibility of developing a product that can identify artificial radionuclides nearby using inexpensive radiation sensors that are easy to use by the public. Therefore, it can contribute to reduce the anxiety of the public exposure by determining the presence of artificial radionuclides in the vicinity.
IntroductionThe general public is afraid of exposure to radiation accidents in places such as nuclear power plants or radiation irradiation facilities that may occur in case of emergency. To confirm this, it is necessary to confirm whether the personal exposure is caused by an artificial radionuclide. However, the radio isotope analysis instrument is difficult to purchase because it is expensive for general use. Therefore, in this study, we developed a gamma energy identification algorithm that can be applied to relatively inexpensive spectroscopy sensors that have low energy resolution than high-resolution sensors for professional use such as the high purity germanium (HPGe) detectors in order to reduce the fear of radiation exposure of the general public.
To confirm the existence of radiation by artificial radio isotopes, the energy of gamma rays has to be identified via a spectral decomposition method for the measured energy spectra [1–4]. HPGe detectors can be used to measure energy spectra due to its extremely high energy resolution, but this is too expensive and complicated for public use [3, 5]. Because of this reason, a compact radiation sensor composed of a 3 mm cubic CsI (Tl) scintillator and a silicon pin photodiode is suggested to measure energy spectra and can be integrated into personal mobile devices such as tablets or smart phones, although the energy resolution of a CsI (Tl) scintillator is lower than that of a HPGe detector. A silicon pin photodiode is very cheap and thin (~800 μm), but it is sensitive to electromagnetic noise due to its unity gain [5]. To compensate for the unity gain of a silicon pin diode, a CsI (Tl) scintillator which has a relatively high light yield among inorganic scintillators and a high effective Z-number (54)1) is suggested. Due to good optical matching, various applications and back-end measurement instruments for this combination have been studied for decades. The spectroscopic characteristic of the subcentimeter-sized CsI (Tl) scintillator was investigated in the previous study [6].
Materials and Methods1. Experimental measurement apparatusThe compact radiation sensor is composed of a CsI (Tl) scintillator cube with one side of 3 mm and a silicon pin photodiode to develop personal radiation measuring instruments. The CsI (Tl) scintillator2) used in this study was manufactured by Epic crystal. It was covered almost entirely with 0.4 mm thick TiO2 reflector, with the exception of the light output surface on the photodiode. The silicon pin photodiode was S1223-013), developed by Hamamatsu (Hamamatsu, Japan). It has an active area of 3.6×3.6 mm2. The A2504) preamplifier was developed by Amptek (Bedford, MA), and the printed circuit board for the compact radiation sensor and the preamplifier was Amptek’s PC2505). The shaping amplifier was a Spectroscopy Amplifier 672, Ortec6)(Oak Ridge, TN). The MCA was PCI Trump Multichannel Buffer, Ortec, which has 2048 channels of spectral bin. Finally, the data acquisition software used was MAESTRO, Ortec.
A source was placed on the vertical top direction of the scintillator, and the distance between the center of the source and the CsI (Tl) scintillator was 30 mm. The activity of the seven types of sources was 23.7 μCi, and the measurement times of the energy spectra were 10, 60, 300, 600, 1,200, 1,800, 3,600 seconds to estimate the performance of the algorithm depending on the fluence of incident radiation. The specification of the sources used for the energy spectrum measurement is listed in Table 1.
2. Gamma energy identifying algorithmThe spectral decomposition converts the measured energy spectrum to the magnitude set of interested gamma energies to be identified. Each magnitude represents the composition ratio of each energy of radiation in the energy spectrum. And, the value of magnitude can be the measured count or the normalized count of gamma energies depending on the calibration matrix in the equation of the spectral decomposition. The meaning of the magnitude in this paper is the normalized count of radiation energy constituting the energy spectrum. The range of the interested gamma energy to be identified is from 20 keV to 1.5 MeV. This range was decided by considering the international criteria for personal monitoring instruments recommended in International atomic energy agency (IAEA) [7]. The magnitude set does not consist of only original gamma energy, but also include incorrect gamma energy which does not exist in the measuring environment. The magnitude of this incorrect gamma energy is defined as modeling error in this study. The ideal value of magnitude of modeling error is zero, but it can positively or negatively increase when the difference between the simulated energy spectrum and the measured energy spectrum for the same gamma energy is large. The simulated energy spectrum cannot compensate electronic noise because the measurement location is various for the mobile detector. Thus unexpected signals as a magnitude of modeling error deteriorate the performance of the algorithm. In this study, a smoothing method is suggested to enhance the performance of the gamma energy identifying algorithm by reducing the magnitude of modeling error in the magnitude set. There are two performance parameters to estimate the contribution of the smoothing method. The first is the accuracy of expected gamma energy and is estimated as the difference between the expected gamma energy in comparison to the original gamma energy. The expected gamma energy is defined as the gamma energy which is expected to be original energy as calculated by the algorithm. The second is the number of repeated calculations in the algorithm needed until proper identification of the two dominant gamma energies in the measured energy spectrum.
The gamma energy identifying algorithm is a three-step of refinement process. Firstly, the magnitude set is calculated by the spectral decomposition. The equation of the spectral decomposition can be expressed as Equation 1 [1, 2].
(1)where S is the magnitude set consisting of the magnitude of the gamma energy, M. And, C is the calibration matrix composed of simulated energy spectra, U is the measured energy spectrum of the unknown source. The number of columns in the C and U from 1 to 2,048 is the order of spectral bin energy in the energy spectrum. The number of rows from 20 keV to 1,500 keV in C is the original gamma energies we are interested to be identifying. The interested gamma energy range can be easily extended by adding the simulated energy spectra in the calibration matrix. The simulated energy spectra in C were repeatedly calculated at 10 keV interval from 20 keV to 1,500 keV using Monte Calro N-Particle code (MCNP7)). In the MCNP simulation, the sensor geometry was same as the measurement equipment using the composition of a CsI (Tl) scintillator and a silicon pin diode. And the radiation source emits the mono energy radiation was set as parallel beam on the scintillator surface. The product of the pseudo-inversed matrix C and the measured energy spectrum, U, is the magnitude set, S.
Secondly, the magnitude of modeling error in the magnitude set is reduced by the smoothing method. The magnitudes indicating the original gamma energy are distributed with positive values in the range of its full width half maximum (FWHM) due to the spectral characteristic of the CsI (Tl) scintillator, while most magnitudes of modeling error are alternately distributed in positive and negative values. The smoothing method reduces the magnitude of modeling error by averaging the two magnitudes in adjacent gamma energy. The equation of the smoothing method can be expressed in terms of magnitude, M, and enhanced magnitude, N, as Equation 2.
where E is the original gamma energy, and i is the order of each magnitude from 20 keV to 1,500 keV in the magnitude set.
Thirdly, the expected gamma energy is finally decided based on the enhanced magnitude set as a result of the spectral decomposition with the smoothing method. To calculate the expected gamma energy, added magnitude is defined as the sum of the enhanced magnitudes in the range of FWHM of the particular gamma energy. Most of the added magnitude indicating the incorrect gamma energy is close to zero with a standard deviation of ±0.06, as confirmed in the measurement results in the next chapter. Thus, the threshold is set to 0.1 based on normalized magnitude. Energy which has a higher added magnitude than this threshold is classified as an expected gamma energy, and all other gamma energy with an added magnitude lower than this threshold is disregarded. The added magnitude indicating the original gamma energy is calculated as 1 when there is little difference between the normalized simulated energy spectrum and the measured energy spectrum of the same gamma energy.
Unit calculation is determined by calculating the added magnitude and comparing it with the threshold. Unit calculation is then used to decide the expected gamma energy and is repeatedly calculated with the magnitude sorted in descending order. This is because gamma energy with high magnitude has a high possibility of indicating the original gamma energy; thus, the added magnitude is centered around this high magnitude gamma energy, and the magnitudes included in the previous calculation are excluded in the next calculation.
The performance of the original spectral decomposition and the spectral decomposition with the smoothing method are compared in terms of the accuracy of expected gamma energy and the number of repeated calculations needed until the two dominant gamma energies of each source are found. The accuracy of expected gamma energy is estimated by the average discrepancy of each gamma energy using Equation 3,
where A.D. is the average discrepancy between the expected gamma energy and the original gamma energy, n is the number of measurements for the measured energy spectra, EO is the original gamma energy, and Ee is the expected gamma energy calculated by the original spectral decomposition or the spectral decomposition with the smoothing method.
3. MCNP simulationThe energy spectra for the calibration matrix in Equation 1 were simulated by MCNPX from 20 keV to 1.5 MeV with every 10 keV step [9]. The FWHM set by considering the energy resolution of the three gamma energies measured by the spectroscopy system suggested in this study (37.6% of 0.059 MeV (241Am), 5.1% of 0.662 MeV (137Cs), and 1.6% of 1.33 MeV (60Co). These energy resolutions are common values using a CsI (Tl) scintillator [8]. The equation to set the FWHM in MCNP is expressed as Equation 4,
where E is the gamma energy (MeV), and a, b, and c are constant as 0.02, 0.0296, and 0.0281, respectively [13]. The activity in the simulation was set to 1 Bq to convert the absolute response probability to spectral bin count to be matched with any activity. Each energy spectra was normalized before being placed in the calibration matrix. The absolute response probability of the photo peak under 100 keV of the original gamma energy decreased because part of the low energy gamma radiation was absorbed by the TiO2 reflector. The simulated energy spectra from 20 keV to 1,500 keV are shown in Figure 1. The X-axis is gamma energy, the Y-axis is spectral bin energy, and the Z-axis is absolute response probability.
Results and DiscussionPrior to estimating the performance of the algorithm, the smoothing method was applied to the magnitude set to confirm the decrease of the magnitudes of modeling error. The specification of the sources used for the energy spectrum measurement is listed in Table 1. The magnitude set calculated by the original spectral decomposition for the measurement results of the 137Cs source is shown in Figure 2. The maximum magnitude was 660 keV of the gamma energy on the x-axis, and the other magnitudes of around 660 keV in the energy range of the FWHM (30 keV) were distributed with positive values. The magnitudes of modeling error are distributed all over the interested gamma energy range. The enhanced magnitude set with the smoothing method is shown in Figure 3. The standard deviation of the magnitude set of the spectral decomposition with smoothing method decreased by 35.8% when compared with the magnitude set of the original spectral decomposition, while the added magnitude indicating the 660 keV changed very little.
One of the key performance parameters, the accuracy of the expected gamma energy, was estimated by the average discrepancy in Equation 3. When using sources which emit multiple gamma rays, the average discrepancy were separately estimated for the two dominant gamma rays. The average discrepancy of each energy of gamma radiation are shown on Figure 4. The solid black bars represent the average error using the original spectral decomposition, and the red bars patterned by diagonal lines indicate the average error using the spectral decomposition with the smoothing method. There are two parameters that affect the average error. The first is the mass attenuation coefficient depending on the original gamma energy. The average error became worse with increasing original gamma energy because the low mass energy attenuation coefficient of the high energy gamma rays made the measured energy spectra unclear due to low spectral counts. The other performance parameter is the interference among the simultaneously-measured gamma rays which have similar energies. In the case of 133Ba, the average error of 80 keV was close to zero, but the average error of 356 keV was relatively higher than the average error of the other gamma energies. The energy spectra of 356 keV gamma rays was hard to classify with the other radiation from 133Ba which has similar energy as 384 keV. The average error of 60Co was also higher than the lower energies, however 1,170 keV and 1,330 keV were not hardly interfered between each other than the 356 keV and 384 keV. The average error of 60Co was caused by the low mass attenuation coefficients (1,170 keV (0.051 cm2·g−1) and 1,330 keV (0.048 cm2·g−1) [9]. The average error caused by these two parameters decreased in the whole energy range after applying the smoothing method—it was reduced to zero with 241Am, 57Co, 133Ba, 137Cs and 54Mn and decreased by half with 22Na and 60Co.
We also estimated the second performance parameter, the number of repeated calculations depending on fluence needed to find the two dominant gamma energies of the sources. The estimation results of the seven sources are shown in Figure 5. The original gamma energies of 241Am and 57Co were equally identified by only 1 calculation based on the spectral decomposition (black circles) and the spectral decomposition with smoothing method (red crosses). In the case of 137Cs and 54Mn, which have higher gamma radiation energy than 241Am and 57Co, the number of repeated calculations increased in the low fluence condition, but the spectral decomposition with smoothing method had a smaller number of repeated calculations than the original spectral decomposition. The number of calculations for the source which emits multiple energy gamma radiations such as 133Ba, 22Na and 60Co increased in comparison with other radio isotopes because of the mass attenuation coefficient and the ratio of spectral count between the two energies of gamma rays. Thus a larger number of calculations were needed to identify the two dominant gamma energies. But the number of repeated calculations for these sources also decreased by half after adapting the smoothing method. This means that the performances of the energy identifying algorithm were enhanced by reducing the magnitude of modeling error even in low fluence conditions.
ConclusionA gamma energy identifying algorithm using spectral decomposition and smoothing method for a compact radiation sensor was suggested in this study. The algorithm can be estimated by two performance parameters: the accuracy of expected gamma energy and the number of repeated calculations. After adapting the smoothing method, the original gamma energy was accurately identified with the single energy of gamma radiation. In addition, the average error decreased by half when calculating multiple energies of gamma radiation in comparison to the original spectral decomposition. The number of repeated calculations also decreased by half even in low fluence conditions under 104 (0.09 cm−2). Through the development of this algorithm, we have confirmed the possibility of developing a product that can identify artificial radionuclides nearby using radiation sensors that are easy to use by the public. Therefore, it can contribute to reduce the anxiety of the public exposure by determining the presence of artificial radionuclides in the vicinity.
ACKNOWLEDGEMENTSThis work was supported by the Center for Integrated Smart Sensors funded by the Ministry of Science, ICT & Future Planning as a Global Frontier Project (CISS-2011-0031870) and the KINS (Radiation Technical Trouble Shooting Center Management, A2GB17230).
Notes1) Physical Properties of CsI (Tl), http://www.crystals.saint-gobain.com/CsI(Tl)_scintillator.aspx 2) Datasheet of the CsI (Tl) crystal, http://www.epic-crystal.com/shop_reviews/csitl-scintillator/ 3) Datasheet of the S1223-01 pin diode, https://www.hamamatsu.com/resources/pdf/ssd/s1223serieskpin1050e.pdf 4) Datasheet of the A250 preamplifier, http://www.amptek.com/pdf/a250.pdf 5) Datasheet of the PC250 test board for the preamplifier, http://www.amptek.com/pdf/pc250.pdf 6) Datasheet of Ortec equipments, https://www.ortec-online.com/ References1. Jolliffe IT. Principal component analysis. 2nd Edition. New York, NY, Springer. 2002;10-61.
2. Stapels C, Johnson E, Chapman E, Mukhopadhyay S, Christian J. Comparison of two solid-state photomultiplier-based scintillation gamma-ray detector configurations. Technologies for Homeland Security 2009. Waltham, Massachusetts. May 11–12, 2009.
3. Runkle RC, Tardiff MF, Anderson KK, Carlson DK, Smith LE. Analysis of spectroscopic radiation portal monitor data using principal components analysis. IEEE Transactions on Nuclear Science. 2006;53(3):1418-1423.
4. Fagan DK, Robinson SM, Runkle RC. Statistical methods applied to gamma-ray spectroscopy algorithms in nuclear security missions. Appl Radiat Isot. 2012;70(10):2428-2439.
5. Knoll GF. Radiation detection and measurement. 4th edition. Hoboken, NJ, John Wiley & Sons. 2010;424-437.
6. Yoo H, Joo S, Yang S, Cho G. Optimal design of a CsI (Tl) crystal in a SiPM based compact radiation sensor. Radiat Meas. 2015;82:102-107.
7. International Atomic Energy Agency. Intercomparison of Personal Dose Equivalent Measurements by Active Personal Dosiemters. IAEA-TECDOC-1564. 2007;22-24.
Fig. 1The simulated energy spectra of the interested gamma energy range for the calibration matrix. The energy spectrum at the front is the result of a simulation of 1.5 MeV radiation. There is a photo-peak at 1.5 MeV and back-scattered peak near 0.45 MeV. 
Fig. 3The enhanced magnitude set of the spectral decomposition with the smoothing method for the energy spectrum of 137Cs. 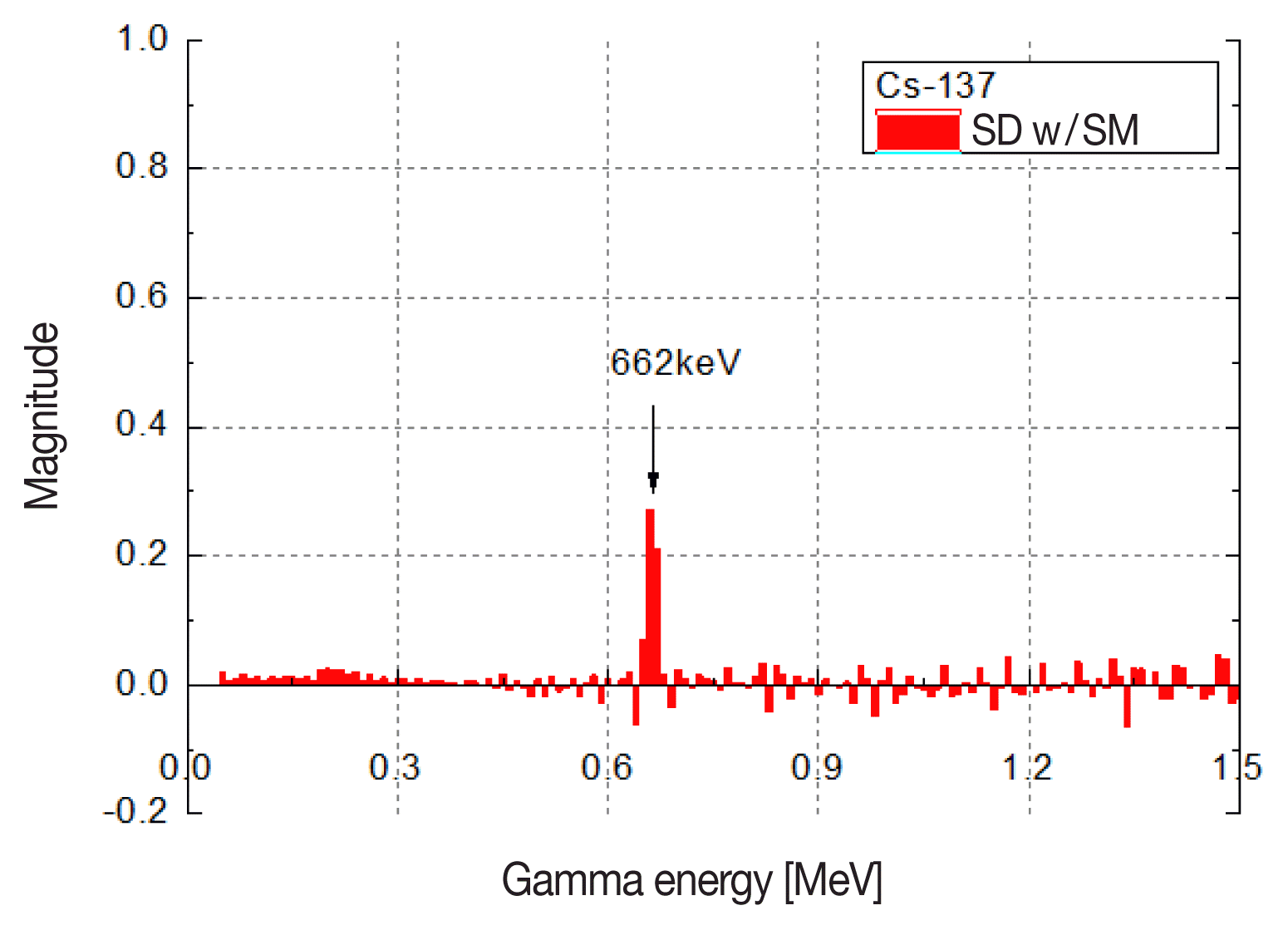
Fig. 4Average discrepancy of expected gamma energy for each original gamma energy. The error bar is the standard deviation of each measurement. 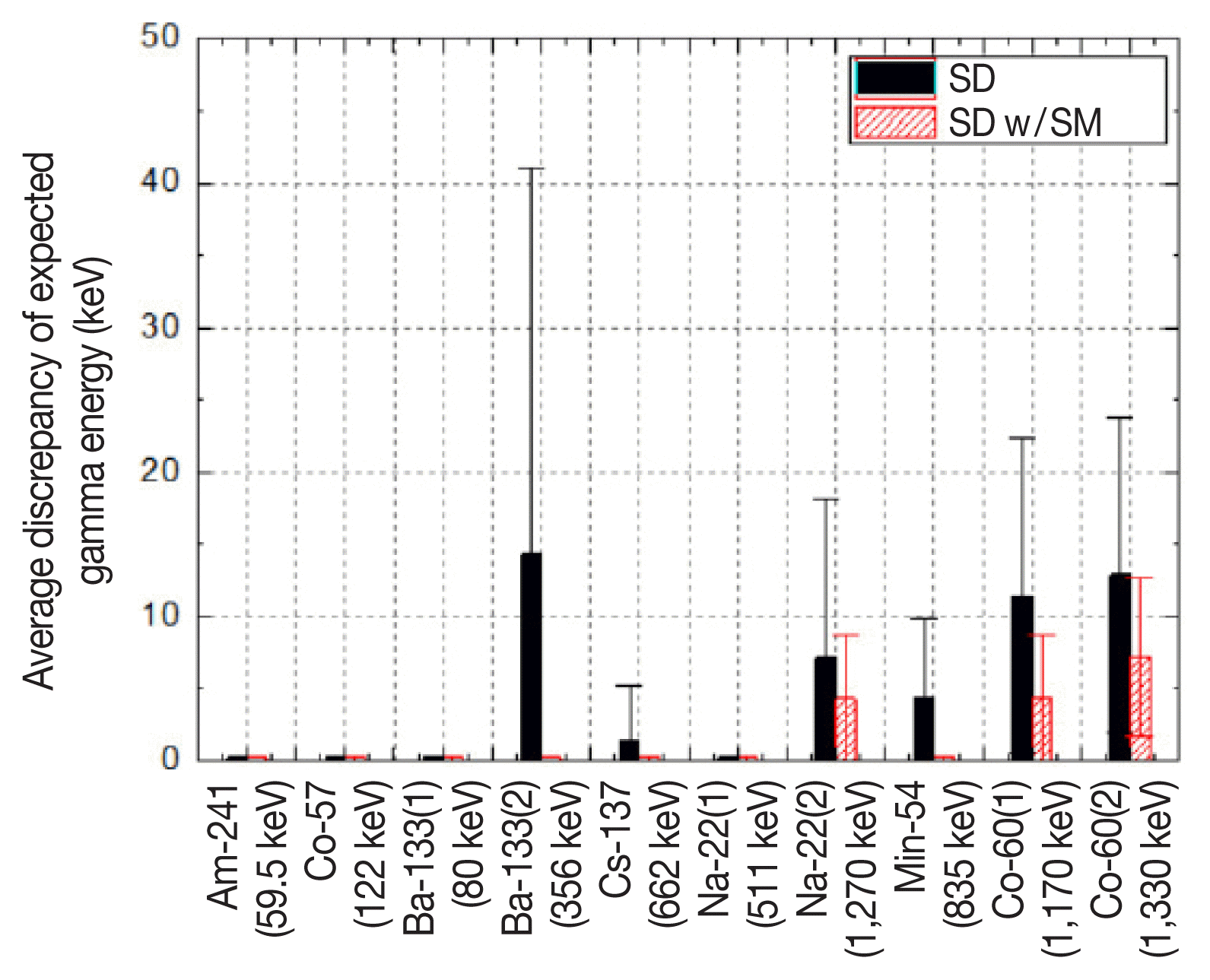
Fig. 5The number of repeated calculations needed to determine the original gamma energy of (A) 241Am, (B)57Co, (C) 133Ba, (D) 137Cs, (E) 22Na, (F) 54Mn, (G) 60Co. 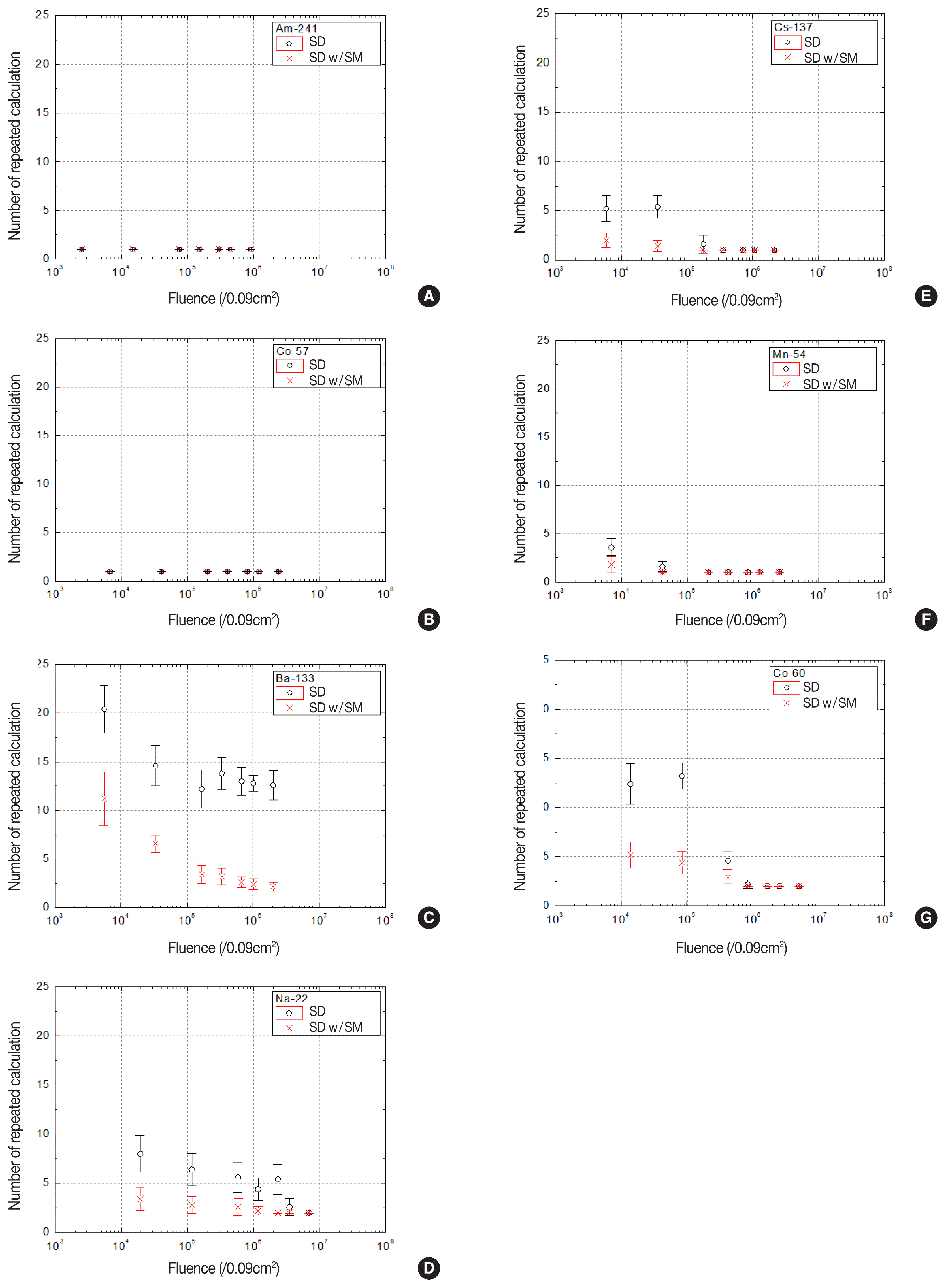
Table 1Specifications of the Radio Isotope Sources |
|
||||||||||||||||||||||||||||||||||||||||