Effect of Heat Treatment on Radiation Shielding Properties of Concretes
Article information
Abstract
Background
Heat energy produced in nuclear reactors and nuclear fuel cycle facilities interactions modifies the physical properties of the shielding materials containing water content. Therefore, in the present paper, effect of the heat on shielding effectiveness of the concretes is investigated for gamma and neutron. The mass attenuation coefficients, effective atomic numbers, fast neutron removal cross-section and exposure buildup factors.
Materials and Methods
The mass attenuation coefficients, effective atomic numbers, fast neutron removal cross-section and exposure buildup factors of ordinary and heavy concretes were investigated using NIST data of XCOM program and Geometric Progression method.
Results and Discussion
The improvement in shielding effectiveness for photon and reduction in fast neutron for ordinary concrete was observed. The change in the neutron shielding effectiveness was insignificant.
Conclusion
The present investigation on interaction of gamma and neutron radiation would be very useful for assessment of shielding efficiency of the concrete used in high temperature applications such as reactors.
Introduction
Wide varieties of radiation shielding materials are being used in nuclear technology for exposure control of occupational radiation workers. The shielding materials are being chosen based on the requirements, application, feasibility, type of radiation, cost, availability, etc. Concrete is one of the most suitable shielding materials in view of cost effective, easily available, easy fabrication of different densities for stopping both the gamma and neutron. The concrete has combination of low- as well as high atomic number elements (H, C, O, S, Ca, Fe) to reduce gamma as well as neutron radiations, which is the most necessary for a nuclear facility. The aggregates increase the density of concrete which results in improvement of shielding efficiency [1–3]. The density is mass of constituent elements per unit volume i. e. increase in density signifies large number of target atom for interaction with incoming radiation.
The concrete is being used for biological shielding of the reactor core and other applications for exposure control. Thermal energy is transferred to the concrete from directly from reactor core as well as radiation interacting with it. Exposure of the concrete with thermal energy modifies physical properties as a result of which elemental composition of the concrete vary. Due envisagement of thermal energy transfers to the biological shielding, the concrete is being cooled by flowing water in contact with it to reduce the temperature. However, the heat transferred to the concrete induces thermal expansion, defects in addition to dehydration of concretes. These effects of heat transferred into the concrete alter chemical compositions of the concrete [4]. Modification in chemical composition due to dehydration of the concrete changes the shielding effectiveness of the concrete used in the nuclear facility. Therefore, it is very essential to have knowledge of effect of heat on shielding properties for the concretes. Few studies are available for investigation of some parameters of concretes under different heat treatment conditions [4]. However, comprehensive investigation on shielding properties of the concretes for heat treatment is not available in literature. This has encouraged our group for investigation of shielding properties of the concretes. This is first attempt to investigate the gamma and neutron shielding parameters of a material under the heat treatment as an external influencing agent for shielding efficiency.
The aim of present study is to investigate shielding effectiveness of heat treated ordinary and high density concretes for gamma and neutron radiations. In present study, shielding parameters viz. mass attenuation coefficients, effective atomic numbers, fast neutron removal cross-section and exposure buildup factors were computed [3, 5–7]. The mass attenuation coefficients using XCOM program were also compared with MCNPX simulation results. The results of the present investigation would be very useful for proper decision of the concrete shielding for use in high temperature applications.
Materials and Methods
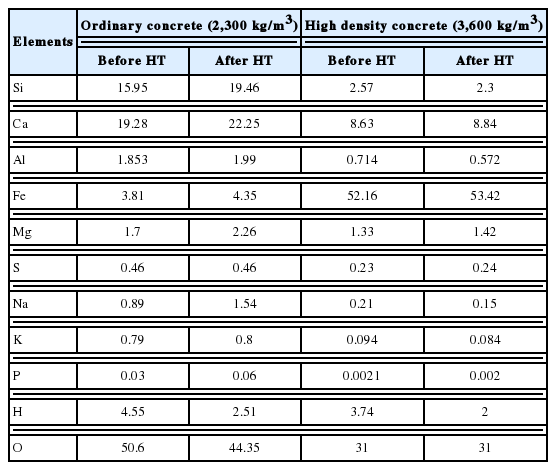
The concrete samples for the present investigation are ordinary concrete (density: 2.3 g/cm3) and high density concrete (density: 3.6 g/cm3). These samples were heated up to 120°C to investigate the effect of heat on shielding properties. Elemental compositions of the concretes before and after the heat treatment are given in Table 1 [4]. It is to be noted that the chemical compositions of the concrete before and after heat treatment change at large extend. These variations in chemical composition lead to alteration of shielding properties.
1. MCNPX code
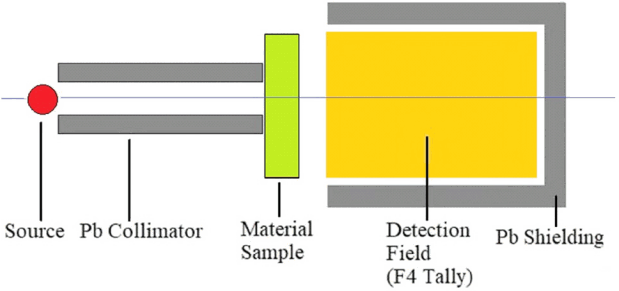
Nowadays, it is becoming very popular to investigate the shielding properties of a material by using the Monte Carlo method. Gamma ray transmission method based on calculating the photon attenuation for a material is applied for evaluation of shielding. Thus, we have applied Monte Carlo N-Particle Transport Code System-extended (MCNPX) version 2.4.0 of Los Alamos national lab (Los Alamos, NM) for investigation of mass attenuation coefficients of investigated concrete samples. MCNPX is a Monte Carlo code for simulation of radiation interactions at wide energy range. MCNPX is fully three-dimensional and it operates extended nuclear cross section libraries and uses certain physics models for different particle types. MCNPX is a major and powerful code for photon attenuation and energy deposition studies. The mass attenuation coefficients for the concrete samples have been calculated for both conditions before and after heating. Similar to the present study, various simulation studies using MCNPX for different radiation applications are found in the literature [8–12]. Simulation parameters such as cell specifications, surface specifications, material specifications and position determinations of each simulation tools have been defined in input file according to the experimental set-up as shown in Figure 1.
In this study, material features have been employed twice. In the first case, elemental mass fractions and density was taken into consideration for the situation before the heating. Secondly, the same calculation has been done for the situation after the heating. In this study, gamma ray sources with various energies were considered as a point isotropic source. The source has been defined in the mode card of MCNPX input file as a point isotropic source at photon energies of 1, 2, 3, 4, 5, 6, 7, and 8 MeV. The absorbed dose amount in the detection field have been obtained by using the average flux tally F4 has been employed. This type of tally in MCNPX scores average flux in a point or cell. In addition, 108 particles have been tracked as the number of particle (NPS variable). MCNPX calculations were done by using Intel® CoreTM i7 CPU 2.80 GHz computer hardware. During the simulation study, the relative error rate has been observed less than 1% of the output file.
2. Theoretical estimation
1) Mass attenuation coefficients
When a beam of monochromatic gamma ray is attenuated on matter according to Lambert-Beer law:
Where, I0 and I are the incident and transmitted photon intensities, respectively, μ (cm−1) represents linear attenuation coefficient of the material and t (cm) is the thickness of the target material. Rearrangement of Equation 1 yields the following equation for the linear attenuation coefficient:
Considering density for gamma interaction, the mass attenuation coefficient is defined and is calculated using the following equation.
Where, wi is the weight fraction, (μ/ρ) is the mass attenuation coefficient of the material, μm is mass attenuation coefficient of element. The wi can be defined as follows:
Where, Ai is the atomic weight of the sample, ni is a number of formula units. The mass attenuation coefficient of elements is taken from National Institute of Standards and Technology (NIST) using XCOM program.1) The XCOM program provides mass attenuation coefficient of elements for gamma energy 1 keV to 100 GeV and using these data the mass attenuation coefficients of compounds or composites have been computed.
2) Effective atomic numbers
Effective atomic cross section, σa, were calculated using the following equation [13]:
Total electronic cross section, σe, has been calculated by:
where fi indicates to the fractional abundance of the element i and Zi the atomic number of the constituent element. The effective atomic numbers (Zeff) is related to σa and σe through the following equation:
3) Exposure buildup factors
Exposure buildup factor (EBF) values and the Geometric Progression (GP) fitting parameters of the concrete samples were computed by method of logarithmic interpolation using the equivalent atomic number (Zeq). The computational work of these parameters is divided in three steps as;
Calculation of equivalent atomic number
Calculation of GP fitting parameters
Calculation of buildup factors
Zeq, is a parameter which describes the concretes properties in terms of equivalent elements similar to atomic number for a single element. Since interaction processes (photoelectric effect, Compton scattering and pair production) of gamma ray with matter are energy dependent, therefore Zeq for the concretes varies according with energy and types of concrete. The photoelectric absorption and pair production are complete removal and removal and regeneration processes, therefore the buildup of photons in the concrete samples is mainly due to multiple scattering events by Compton scattering, so that Zeq is derived from the Compton scattering interaction process to understand buildup phenomenon.
The Zeq, for each concrete sample is estimated by the ratio of (μ/ρ)Compton/(μ/ρ)Total, at a specific energy. Thus first the Compton partial mass attenuation coefficient, (μ/ρ) Compton and the total mass attenuation coefficients, (μ/ρ) Total are for the concrete samples in the energy region 0.015 to 15 MeV using XCOM [13]. The logarithmic interpolation of Zeq is employed by formula [14]
where Z1 and Z2 are the atomic numbers corresponding to the ratios R1 and R2 respectively.2) R is the ratio, (μ/ρ)Compton/(μ/ρ)Total at specific energy and the ratio (μ/ρ)Compton/(μ/ρ)Total for Zeq lies between two successive ratios.
The GP fitting parameters are calculated in the similar fashion of logarithmic interpolation procedure for Zeq. The GP fitting parameters for the elements were taken from the ANS, 1991 standard reference database.3)
Third and final step is buildup factors estimation by GP fitting parameters (b, c, a, Xk, and d) in the photon energy range of 0.015 to 15 MeV up to a 40 mfp by equations [15, 16] as
where X is the source-detector distance in terms of mfp and b is the value of the EBF at 1 mfp, K (E, x) is the dose multiplicative factor, and b, c, a, XK, and d are computed GP fitting parameters which depends on the attenuating medium and source energy. The Zeq of the concretes is given in Table 3.
4) Macroscopic effective neutron removal cross-section
The effective removal cross-section for fast neutron (2–12 MeV) for compounds and homogenous mixtures may be calculated by mixture rule.4), The effective linear removal cross-section ∑R (=∑iρi×(∑R/ρ)i) in unit of cm−1 where ρi is partial density of the element of the concrete sample. The values obtained for ∑R/ρ by above equation are accurate within 10% of the experimental values investigated for aluminum, beryllium, graphite, hydrogen, iron, lead, oxygen, boron carbide etc.5), The ∑R/ρ values of elements have been taken from Kaplan and Chilton.6,,7)
Results and Discussion
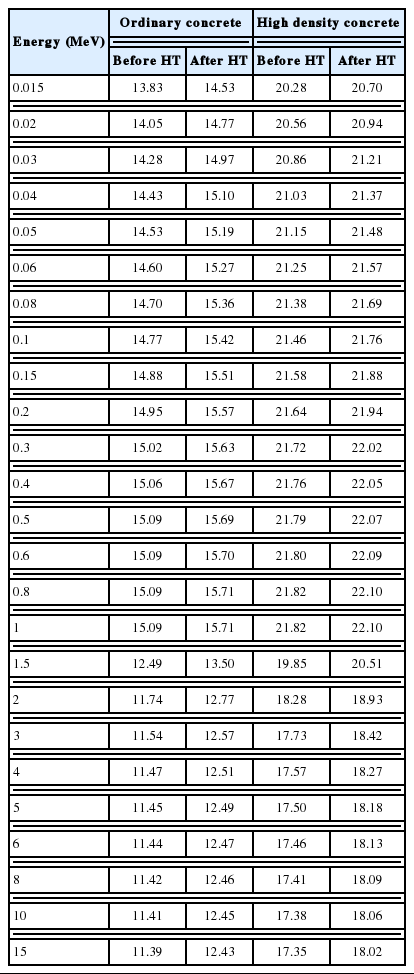
The mass attenuation coefficients, effective atomic numbers, neutron removal cross-sections and exposure buildup factors for ordinary and high density concrete samples are shown in Figures 2–5. The mass attenuation coefficients for the ordinary and high density concrete samples simulated using MCNPX are given in Table 2.
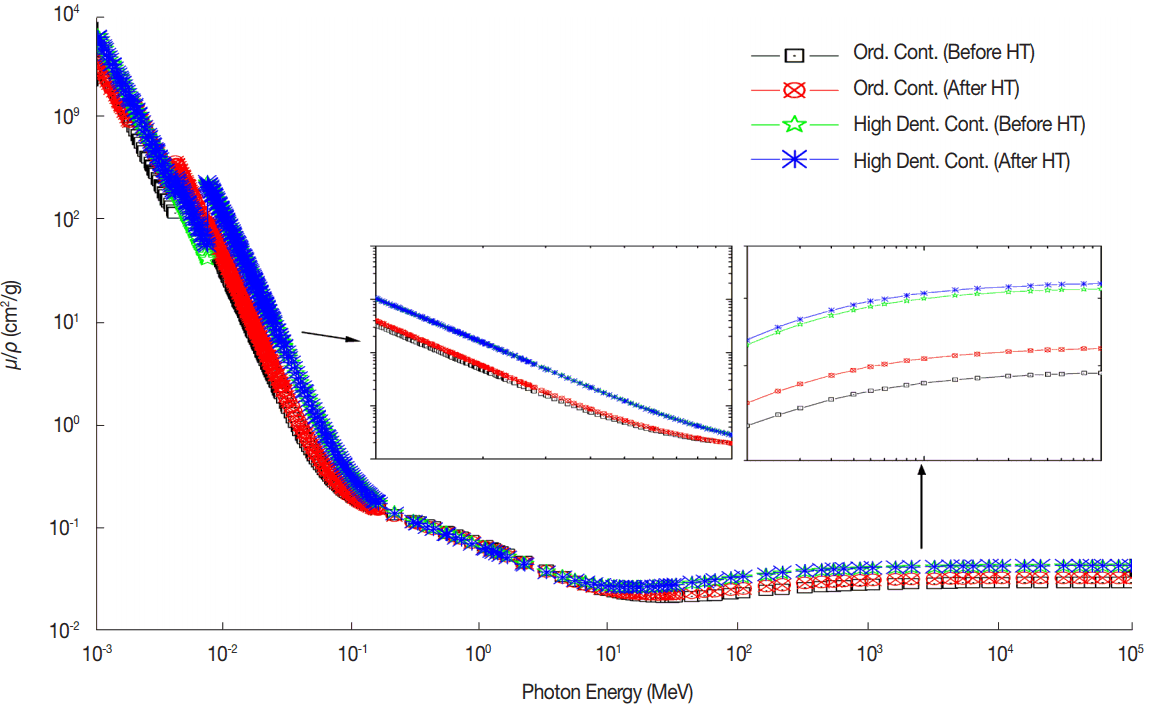
Mass attenuation coefficients of ordinary and high density concretes before and after heat treatment.
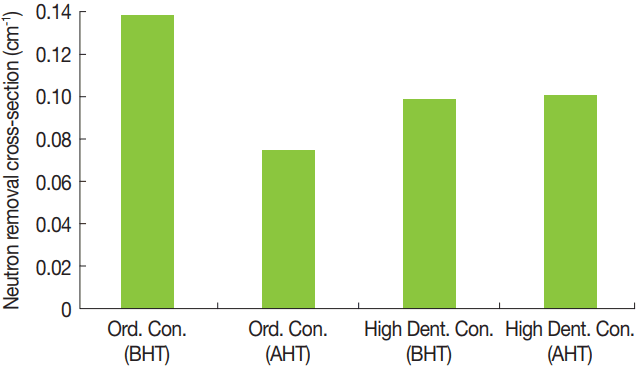
Fast neutron removal cross-section of ordinary and high density concretes before and after heat treatment.

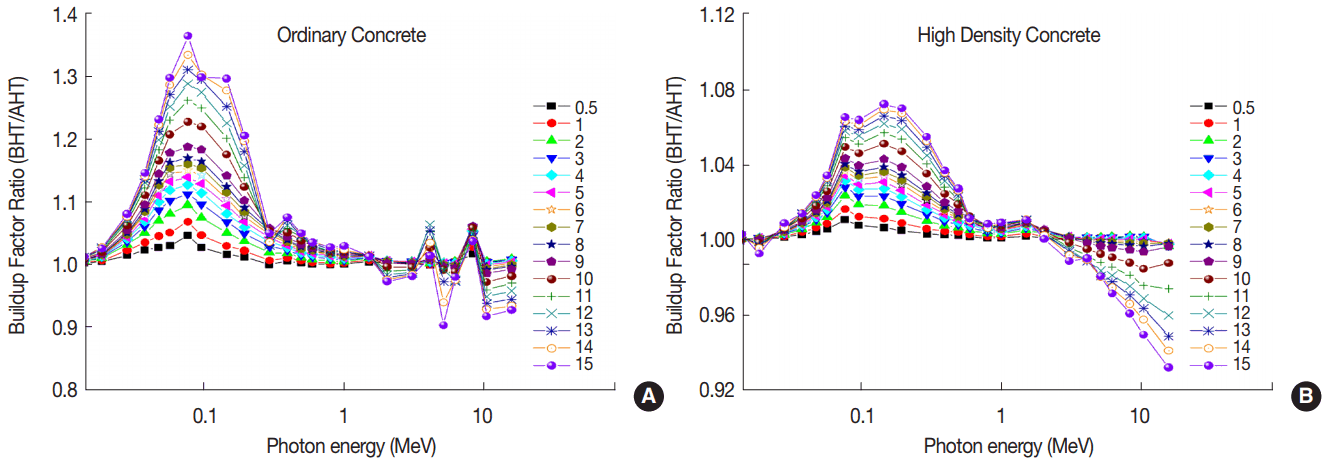
Exposure buildup factors of ordinary and high density concretes before and after heat treatment (A) 5 mfp (B) 10 mfp (C) 20 mfp (D) 40 mfp.
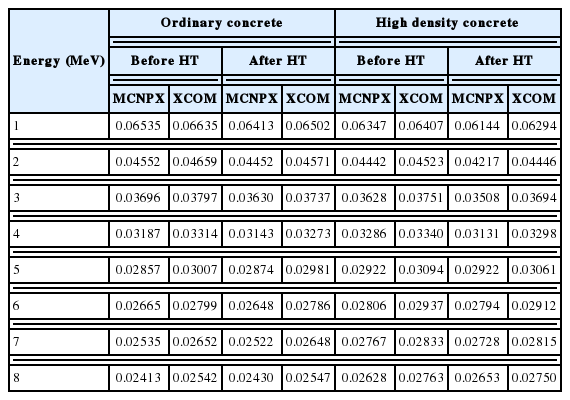
Mass Attenuation Coefficients of Ordinary and High Density Concretes before and after Heat Treatment Using MCNP Simulation and XCOM
1. Mass attenuation coefficients
In Figure 2, mass attenuation coefficient (μ/ρ) values of the concrete samples are shown for photon energy rage 1 keV to 100 GeV. The large variation of μ/ρ values of the concrete samples is to be observed and it is divided in three parts as low (E<100 keV), medium (100 keV<E<3 MeV) and high-energy (E>3 MeV) regions. The ordinary concrete sample are showing lesser μ/ρ values than high density concrete sample because ordinary concrete contains lesser composition of high atomic number elements. The variation in low energy region is very sharp increase and decrease of the coefficients with increase in energy. The variation in explained by photo electric effect where interaction cross-section is dependent upon photon energy and atomic number as Z4–5/E7/2. The variation in medium energy region is explained by Compton scattering where interaction cross-section is approximately independent upon photon energy and depend upon atomic number only. In high energy range, the variation of μ/ρ values is due to dependency of interaction cross-section as Z2. The μ/ρ values for few selected energies were computed using MCNPX, compared with XCOM and given in Table 2. It can be noted that the μ/ρ values using MCNPX are comparable with NIST using XCOM program. Here it is concluded that the MCNPX is capable of simulation for radiation interaction in presence of external interfering agent.
It is to be noted that the μ/ρ values for the ordinary and high density concretes are lesser before heat treatment and increases after the heat treatment. It can be concluded that the heat treatment marginally increases shielding effectiveness.
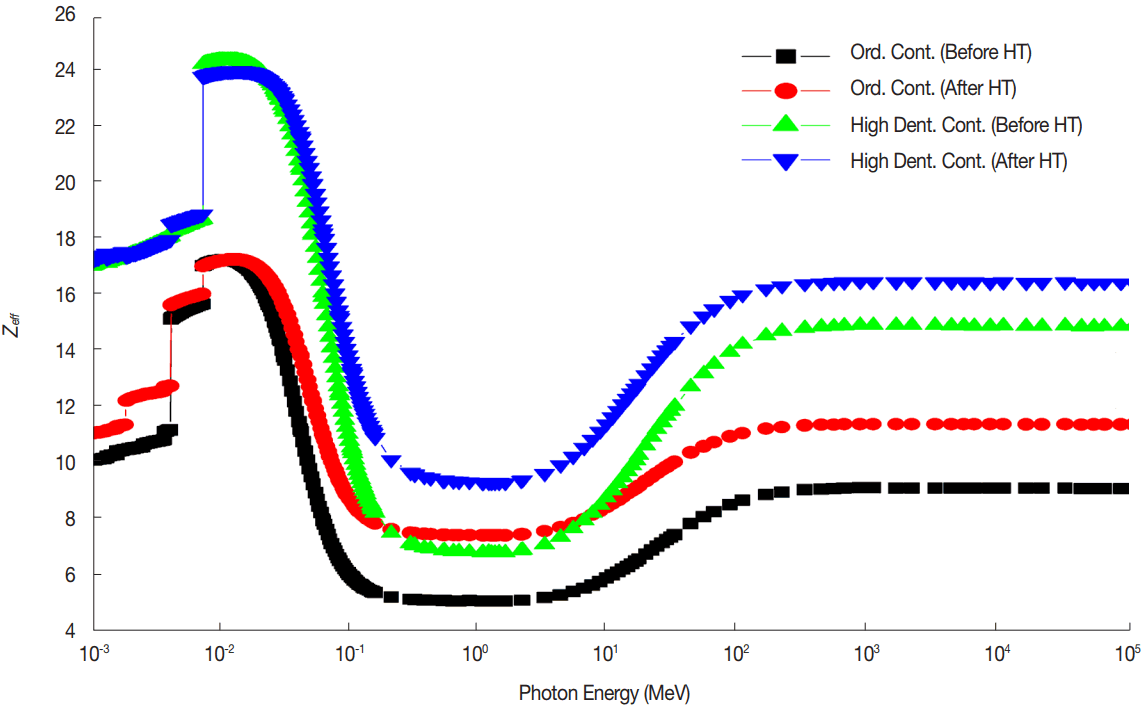
2. Effective atomic numbers
In Figure 3, the effective atomic number (Zeff) of the concrete samples is shown for photon energy rage 1 keV to 100 GeV. The variation of Zeff with photon energy is similar to the μ/ρ values, therefore it can be explained by photoelectric effect, Compton scattering and pair production interaction processes.
It is to be noted that the Zeff for the ordinary and high density concretes are lesser before heat treatment and increases after the heat treatment. Therefore, it concluded that the heat treatment marginally increases shielding effectiveness for the concrete samples.
3. Macroscopic effective neutron removal cross-section
Figure 4, neutron removal cross-section for the ordinary and high density concretes are shown before and after heat treatment. It is to be noted that fast neutron removal cross-section for the ordinary concrete reduces significantly after heat treatment, whereas insignificant change for the high density concrete.
The low atomic number elements are dominant conscientious for shielding of fast neutrons (2–12 MeV). Therefore, significant reduction of chemical composition of low atomic number elements (H and O) after heat treatment (see Table 1) is major reason for large variation of ∑R value for ordinary concrete sample. At same time the variation in chemical compositions of heavy concrete samples are insignificant, which results in unnoticed change of ∑R value.
4. Exposure buildup factors
The variation of exposure buildup factor (EBF) of the concrete samples with photon energy at different mean free paths before and after heat treatment is shown in Figure 5. It is observed that the EBF for the concrete samples are small in low- and high-energy regions and highest in intermediate medium energy region for both the conditions of before and after heat treatment.
The reasons for such variation of EBF can be explained by basic interaction processes i.e. photoelectric effect, Compton scattering and pair production [3, 6, 17]. The EBF values in photoelectric absorption regions are found to be lowest because the after interaction of photon with material, photon completely removes whereas in case of high energy region the high energy photon (>1.022 MeV) removes completely from interaction process and convert into positron and electron. The positron annihilates with electron at rest to generate two photons of lower energy (0.511 MeV). These lower energy photons follow multiple scattering processes for interaction and increase the EBF value in high energy region. In intermediate energy region, photon follows multiple interactions to increase buildup of photon in this region. The explanation for variation of exposure buildup factors with photon energy, chemical composition and thickness can be found elsewhere in various literatures.
The change in EBF due to heat treatment is shown in Figure 6 by ratio of EBF before to after treatment. It is observed that the EBF decrease in low-energy and increases in high-energy region, whereas roughly constant in medium-energy region (Compton scattering). Also, it is to be noted that decrease in EBF in low energy region for ordinary concrete is larger than high density concrete.
Conclusions
In the present investigation on gamma and neutron shielding effectiveness for the ordinary and high density concretes before and after heat treatment, mass attenuation coefficients, effective atomic numbers, and exposure buildup factors are found to be dependent heat treatment. The mass attenuation coefficients for the ordinary and high density concretes are lesser before heat treatment and increases after the heat treatment. The heat treatment of the concrete marginally increases gamma shielding effectiveness. The neutron removal cross- section of the ordinary concrete reduces after heat treatment whereas it is independent for the high density concrete. Also, the MCNPX is capable of simulation mass attenuation coefficients for radiation interaction in presence of heat treatment.
The experimental investigation on shielding effectiveness of the ordinary and high density concretes in under process.
Notes
Berger MJ, Hubbell JH, Seltzer SM, Chang J, Coursey JS, Sukumar R, Zucker DS, Olsen K. XCOM: photon cross sections database, NIST standard reference database (XGAM); 2010. Available at http://www.nist.gov/pml/data/xcom/index.cfm.
Maron MJ. Numerical analysis: a Practical approach. 2nd Ed. New York, NY. Macmillan Publishing Co., Inc., 1987.
Trubey DK, Eisenhauer CM, Foderaro A, Gopinath DV, Harima Y, Hubbell JH, Shure K, Su S. Gamma Ray Attenuation Coefficient and Buildup Factors for Engineering Materials. American Nuclear Society. ANSI/ANS-6.4.3, 1991.
Wood J. Computational methods in reactor shielding. New York, NY. Pergamon Press Ltd., 1982.
Samuel G, Alexander S. Nuclear reactor engineering, 4 (Vol.I). [Edition No.]. Delhi, India. CBC Publishers & Distributors, 2004.
Kaplan MF. Concrete radiation shielding. New York, NY. Longman Scientific & Technical, 1989.
Chilton AB, Shultis JK, Richards EF. Principle of radiation shielding. Englewood Cliffs, NJ. Prentice-Hall, 1984.