Improvement of Statistics in Proton Beam Range Measurement by Merging Prompt Gamma Distributions: A Preliminary Study
Article information
Abstract
Background
To monitor proton beam in proton therapy, prompt gamma imaging systems are being developed by several research groups, and these systems are expected to improve the quality of the treatment and the patient safety. To apply the prompt gamma imaging systems into spot scanning proton therapy, the systems should be able to monitor the proton beam range of a spot with a small number of protons (<108 protons), which is quite often not the case due to insufficient prompt gamma statistics.
Materials and Methods
In the present study, we propose to improve prompt gamma statistics by merging the prompt gamma distributions of several individual spots into a new distribution. This proposal was tested by Geant4 Monte Carlo simulations for a multi-slit prompt gamma camera which has been developed to measure the proton beam range in the patient.
Results and Discussion
The results show that the proposed method clearly enhance the statistical precision of beam range measurement. The accuracy of beam range verification is improved, within ~1.4 mm error, which is not achievable before applying the developed method.
Conclusion
In this study, we tried to improve the statistics of the prompt gamma statistics by merging the prompt gamma distributions of multiple spots, and it was found that the merged distribution provided sufficient prompt gamma statistics and the proton beam range was determined accurately.
Introduction
The main advantage of proton therapy is to deliver a highly conformal dose to a tumor volume in the patient [1] due to its unique dose deposition pattern. The deposited dose reaches the maximum at the distal range of the proton beam, beyond which it sharply falls to almost zero, resulting in so-called distal fall-off of dose distribution. The proton therapy therefore gives higher dose to the tumor and minimal harm to the surrounding healthy tissues, assuming the range of the beam is well controlled and monitored. On the other hand, if the beam range is not accurately controlled, the characteristic of proton dose may result in significant under- or overdoses in tumor or critical tissue near the distal fall-off region.
Prompt gamma imaging, which is based on the distribution of prompt gammas from the proton-induced nuclear interactions in the patient, is considered one of the most promising technologies for proton beam monitoring, mainly due to high correlation between prompt gamma and proton dose distributions in the distal fall-off region [2]. Since our first experimental demonstration of proton beam range measurement with prompt gammas in 2006 [3], different types of prompt gamma detection systems have been proposed by several research groups [4–10]. However, most of these systems still show unsatisfactory performances, mainly due to low detection statistics, especially when we consider spot scanning proton therapy, the most promising technology in proton therapy.
To monitor the spot scanning proton therapy, a prompt gamma detection system should be able to measure the proton beam range of a spot with a small number of delivered protons (<108 protons [11]). This means the detection efficiency of the prompt gamma imaging system should be very high, which is often difficult to achieve due to several practical reasons, including limitation in the size and weight of the detection system for clinical use.
In the present study, we propose to improve the prompt gamma statistics by merging the prompt gamma distributions of several spots into a new distribution. In this study, the proposed method was tested by Geant4 Monte Carlo simulation. In the simulation, the prompt gamma distributions were obtained by a multi-slit prompt gamma camera which has been developed to measure the range of the proton beam in the patient by measuring prompt gammas from the proton beam passage in the patient.
Materials and Methods
1. Merging of prompt gamma distributions
In spot scanning proton therapy, although the number of protons for each spot is small, there are many spots and the total number of protons for an energy layer or for a beam location (i.e. through several energy layers) is very large. In the present study, therefore, we propose to generate a new distribution by summing several measured prompt gamma distributions of multiple spots to improve the statistics of the prompt gamma distribution. The new distribution will have more improved prompt gamma statistics and show reduced coefficient of variance, which enables us to determine the beam range more accurately. The prompt gamma distributions can be merged for the spots in the same energy layer or for the spots at the same beam location. When combining the prompt gamma distributions, the axes of the distributions should be matched up according to the actual beam range to accumulate the prompt gamma counts at the exact axial location.
2. Geant4 simulations
The proposed method was tested using Monte Carlo simulations. For Monte Carlo simulation, Genat4 (ver. 10.03.p01) was used on a computer with the Intel Xeon E5-2697 v2 (@ 2.70 GHz and 256 GB memory). The averaged computation time for an energy layer is about 44 hours with 24 CPU threads. Concerning the physics process in Geant4, the modular physics list, QGSP_BERT_HP, was used to simulate the particle interactions. The cut value for proton, gamma, electron, and positron was set as 1.0 mm. In order to speed up the computation time, we applied particle splitting technique by splitting each secondary proton and neutron, generated from primary protons, into 10 protons and 10 neutrons, respectively. The event biasing technique was applied only in the phantom.
In the simulation, the proton beam was irradiated into a cylindrical phantom and the generated prompt gamma rays were measured using a multi-slit prompt gamma camera (Figure 1). The multi-slit prompt gamma camera consists of a multi-slit collimator and two rows of 36 CsI(Tl) scintillators. The collimator is made with tungsten. The width and septal thickness of the slit is 2 mm which results in 4 mm pitch, and the height and length is 100 mm. The multi-slit collimator is placed in a staggered arrangement to achieve 2 mm slit pitch overcoming physical limitations of the 4 mm slit pitch. Total 72 CsI(Tl) scintillators (4.51 g·cm−3) of 3 mm (thickness)×30 mm (width)×100 mm (height) are placed behind the collimator. Additionally, to shield unwanted radiations (e.g. secondary protons and neutrons) from the sides, we placed tungsten shields at both side of the camera.
Multi-slit prompt gamma camera, cylindrical phantom, and proton beam modeled in Geant4 Monte Carlo code.
The phantom was a homogeneous cylinder with 15 cm and 40 cm of radius and height, respectively, which is made of PMMA (polymethyl methacrylate, density=1.19 g·cm−3). The proton beam was irradiated at the center of phantom in the axial direction (Figure 1). The distance between the phantom surface and the multi-slit prompt gamma camera was 8 cm.
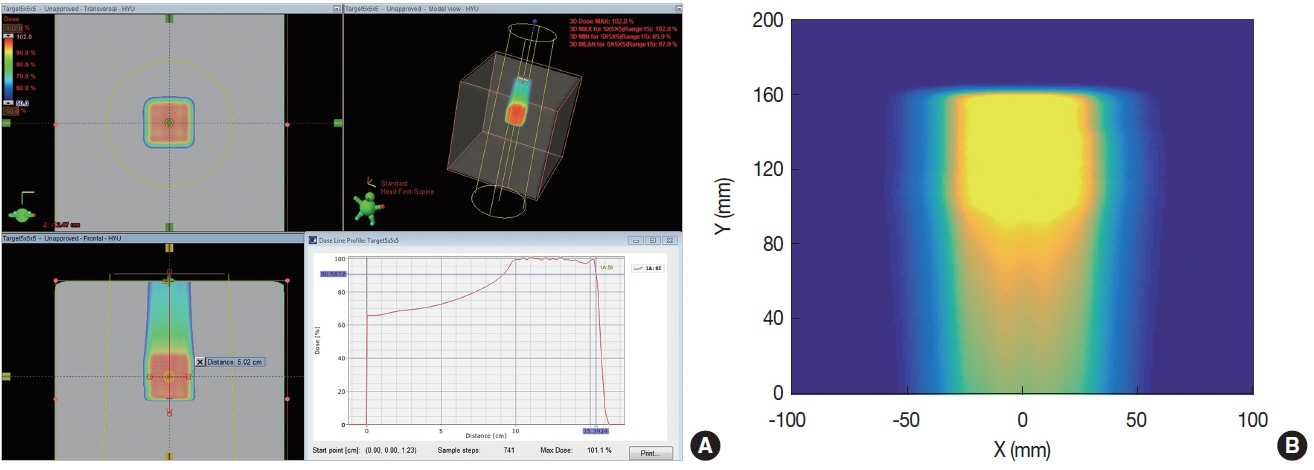
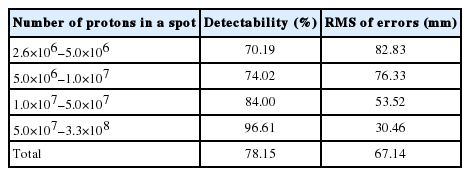
For the dose distribution used in the simulation, we used a single field cubic (5×5×5 cm3) dose distribution planned at the National Cancer Center (NCC) in Korea. To produce the cubic dose distribution, the beam energy was varied from 115.8 to 149.1 MeV. The distribution has total 12 energy layers, and 1,295 spots. The total delivered dose was 2 Gy. Figure 2A shows the planned dose distribution, and Figure 2B shows the dose distribution, which was simulated by Geant4 for same beam condition.
3. Test cases
Before the performance evaluation, we estimated the error in beam range determination without applying the developed method. The beam ranges for every spot in the dose distribution were measured and the differences between the measured and the real beam range were analyzed. In this analysis, the results were classified according to the number of delivered protons into the spots.
The prompt gamma distributions of the spots, measured using the multi-slit prompt gamma camera, were summed in two different ways: (1) summed in the same energy layer; (2) summed at the same beam location. In the first test case, the axes of the prompt gamma distributions did not have to be matched up because the axial locations of the spots were same due to the homogeneity of the phantom. In the second test case, on the other hand, the axes were shifted to the most distal axial point because the axial locations of the spots were different depending on the beam energy. The beam ranges were verified using these merged prompt gamma distributions, and the differences between the determined and the real beam range were estimated.
The beam ranges were determined using an automated proton beam range measurement algorithm developed for multi-slit prompt gamma cameras [12]. In the algorithm, if the prompt gamma statistics is not enough, the algorithm is not applied, and the beam range is not decided either. The probability of successful application of the beam range measurement algorithm, therefore, can be a proper indicator to confirm the improved prompt gamma statistics. In the present study, this probability is defined as ‘detectability’ and used for analysis of the results.
Results and Discussion
1. Precision of beam range determination before applying developed method
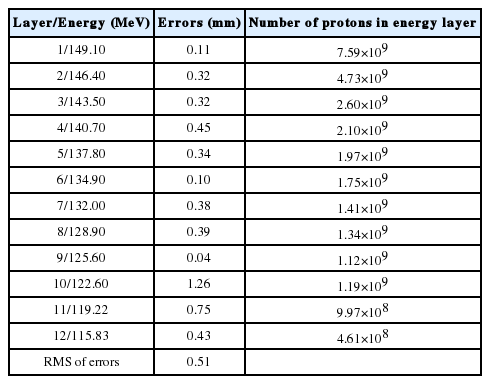
In order to evaluate the precision of beam range determination without using the developed method, we first estimated the beam ranges using the measured prompt gamma distributions of individual spots, and the errors between the measured and the real beam ranges were analyzed (Table 1). For analysis, the spots were divided into four groups according to the number of delivered protons. For each group, the detectability and the root mean square (RMS) of the errors were estimated. Table 1 shows that for the group of the spots with a larger number of delivered protons, the detectability is higher, and the RMS of the errors is smaller. Even for the group of the largest number of protons, however, the RMS of the errors is still unacceptably large (=30.46 mm). Considering the entire spots, the detectability and the RMS of the error are 78.15%, 67.14 mm, respectively, which is unsatisfactory for use in clinics. This result clearly indicates that the prompt gamma statistics should be improved to monitor the proton beam in spot scanning proton therapy.
2. Combination of prompt gamma distributions in the same energy layer
To improve the prompt gamma statistics, the prompt gamma distributions of the spots in in an energy layer were combined to produce a new combined prompt gamma distribution. In this case, the axes of the prompt gamma distributions were not shifted because the axial locations of the spots were same. For this reason, the prompt gamma distributions were simply summed. Figure 3 shows the prompt gamma distributions of individual spots and the merged distribution for the distal energy layer (i.e. 149.1 MeV). It can be seen that the merged distribution shows much less statistical fluctuation than the prompt gamma distributions of individual spots. The fall-off region in the merged distribution can also be clearly identified.

Prompt gamma distributions of individual spots and merged distribution for the distal energy layer (i.e. 149.1 MeV). X and Y axes of the prompt gamma distributions are depth in phantom (from 0 to 400 mm) and prompt gamma counts, respectively.
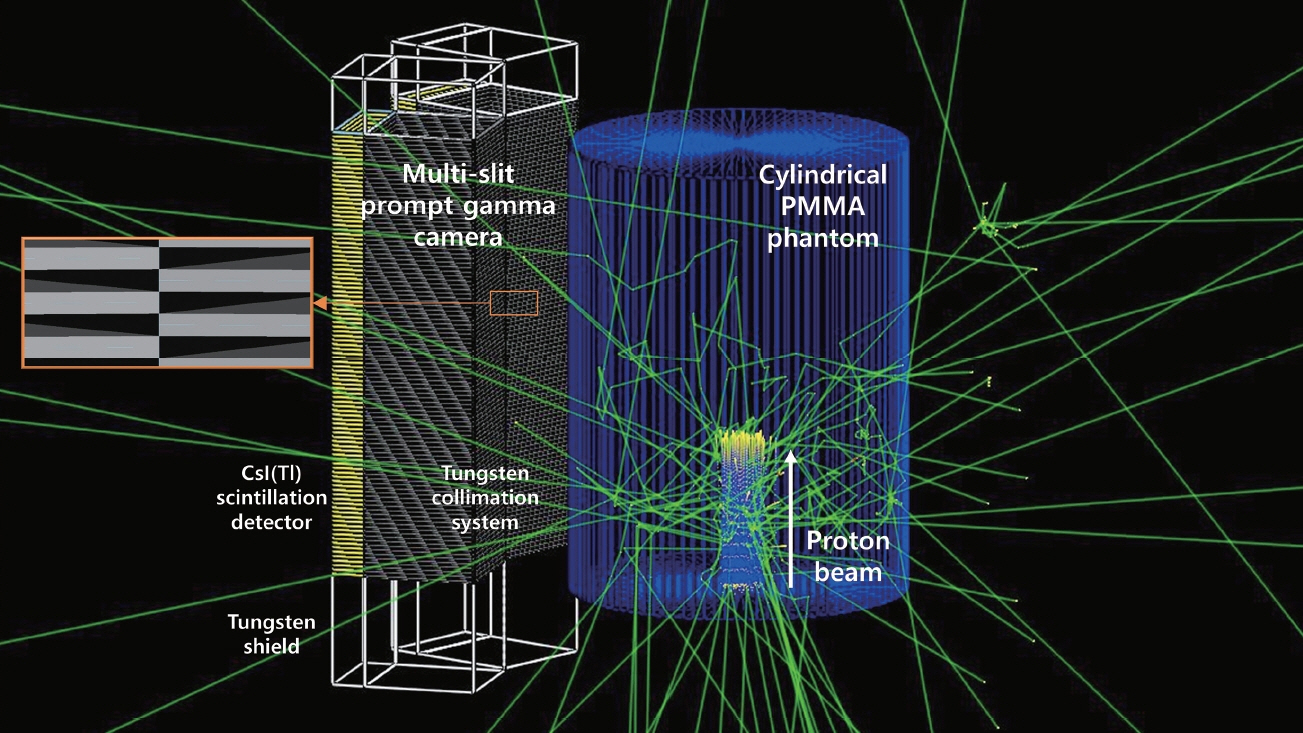
Table 2 shows the errors in beam range measurement for each energy layers after applying the developed method. It can be seen that the errors are now very small (i.e. less than 1.3 mm). The RMS of the errors was only 0.51 mm and detectability was 100% considering all of the energy layers. The results clearly show that the precision of the beam range verification can be substantially improved by summing prompt gamma distributions.
3. Combination of prompt gamma distributions at the same beam location
The prompt gamma distributions were also merged for the spots at the same beam location. In this case, the axes of the prompt gamma distributions were shifted because the axial locations of each spot were different due to different proton energies. All of the distributions were shifted to the most distal axial point and combined together to estimate the beam range of the distal layer.
Figure 4 shows the prompt gamma distributions of individual spots and the merged distribution for the beam location (25 mm, 25 mm). Again, at least for this specific beam location, it can be seen that the merged distribution shows much less statistical fluctuation than the prompt gamma distributions of individual spots and the fall-off region in the merged distribution can also be clearly identified.
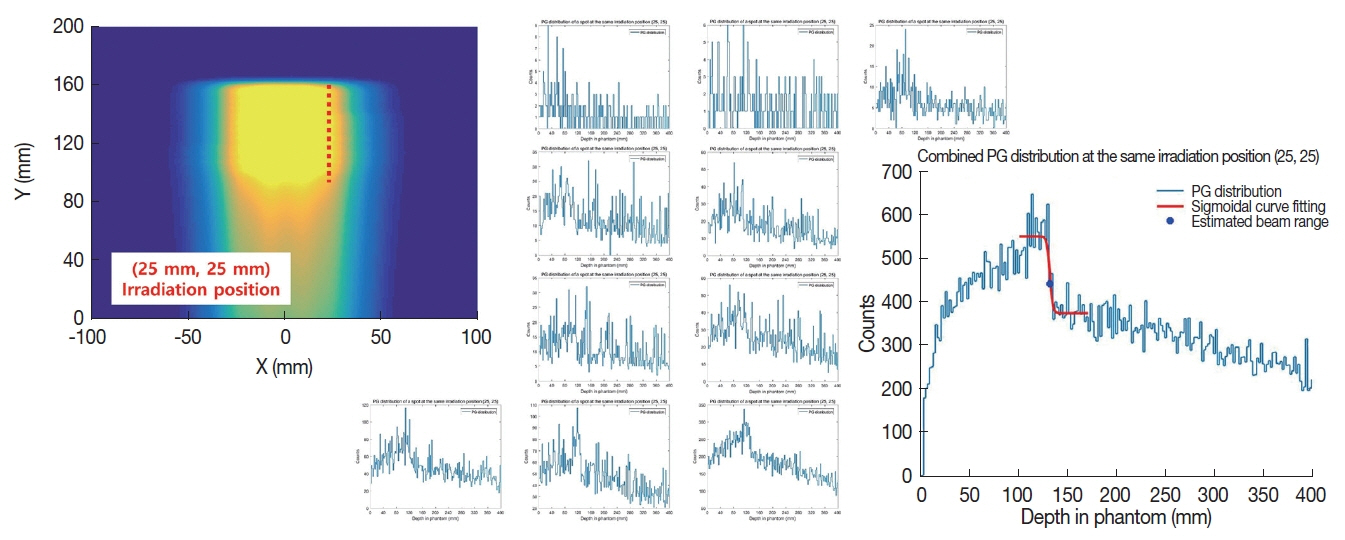
Prompt gamma distributions of individual spots and merged distribution for the beam location (25 mm, 25 mm). X and Y axes of the prompt gamma distributions are depth in phantom (from 0 to 400 mm) and prompt gamma counts, respectively.
Our analysis for all beam locations, however, shows that the beam range is not determined for 7 out of total 159 beam locations due to insufficient prompt gamma statistics, resulting in about 95% of detectability. The RMS of the errors was about 30 mm, which was very large when compared to the previous test cases of merging in an energy layer. The number of spots for more than 2 mm of error was 122 among 152 beam locations (except 7 locations mentioned above), which shows that the prompt gamma statistics is still not enough for most of the beam locations.
Therefore, it was also tried to add extra prompt gamma distributions to improve statistics. For this, at each beam location, the merged prompt gamma distributions of the neighboring eight beam locations were summed to the merged prompt gamma distribution of the beam location. For the beam locations at the boundary, the merged prompt gamma distributions of only three to five beam locations were summed to the merged prompt gamma distribution of the beam location. Our analysis of the results then shows that the prompt gamma statistics is significantly improved by this treatment - the detectability, RMS of error, and the number of spots for more than 2 mm error being 100%, 1.38 mm, and 0 respectively.
Conclusion
In the present study, we tried to improve the statistics of the prompt gamma statistics by merging the prompt gamma distributions of multiple spots. Two different ways were investigated to combine the prompt gamma distributions; adding the distribution of prompt gammas of the spots in the same energy layer and in the same beam location. For the test cases of merging in the same energy layer, it was found that the merged distribution provided sufficient prompt gamma statistics and the proton beam range was determined accurately, within ~1.4 mm error. On the other hand, the improvement of prompt gamma statistics was not enough for the cases of merging in the same beam location, in which case we proposed to sum additional prompt gamma distributions (i.e. the merged prompt gamma distributions of neighboring beam locations). In the test cases of the present study, a homogeneous phantom was used, which made the shift of prompt gamma distributions to produce a new merged prompt gamma distribution simply to be based on the beam range information. In a heterogeneous medium like a human body, however, the shifting should be performed based on the information of the beam range in the heterogeneous medium and it is believed that the CT image of the patient can be used for this. The ways of combining the prompt gamma distributions introduced in the present study were very simple, and the merging of the prompt gamma distributions can be done in more sophisticated ways. For example, the distributions of the prompt gammas can be merged for some variable and optimized combination of spots in three-dimensional space, or the distributions can be merged considering the necessary number of protons to reach a satisfactory statistics. In the future, the performance of this method will be evaluated using heterogeneous phantoms and more sophisticated combination of prompt gamma distributions.
Acknowledgements
This work was supported by the Nuclear Safety Research and Development (NSR&D) Program through the Korea Foundation of Nuclear Safety (KoFONS) funded by the Nuclear Safety and Security Commission (NSSC) (Project Number: 1705006).