Demonstration of the Effectiveness of Monte Carlo-Based Data Sets with the Simplified Approach for Shielding Design of a Laboratory with the Therapeutic Level Proton Beam
Article information
Abstract
Background
There are several proton therapy facilities in operation or planned in Taiwan, and these facilities are anticipated to not only treat cancer but also provide beam services to the industry or academia. The simplified approach based on the Monte Carlo-based data sets (source terms and attenuation lengths) with the point-source line-of-sight approximation is friendly in the design stage of the proton therapy facilities because it is intuitive and easy to use. The purpose of this study is to expand the Monte Carlo-based data sets to allow the simplified approach to cover the application of proton beams more widely.
Materials and Methods
In this work, the MCNP6 Monte Carlo code was used in three simulations to achieve the purpose, including the neutron yield calculation, Monte Carlo-based data sets generation, and dose assessment in simple cases to demonstrate the effectiveness of the generated data sets.
Results and Discussion
The consistent comparison of the simplified approach and Monte Carlo simulation results show the effectiveness and advantage of applying the data set to a quick shielding design and conservative dose assessment for proton therapy facilities.
Conclusion
This study has expanded the existing Monte Carlo-based data set to allow the simplified approach method to be used for dose assessment or shielding design for beam services in proton therapy facilities. It should be noted that the default model of the MCNP6 is no longer the Bertini model but the CEM (cascade-exciton model), therefore, the results of the simplified approach will be more conservative when it was used to do the double confirmation of the final shielding design.
Introduction
Not only the galactic cosmic rays but also the solar cosmic rays, protons account for a large part of the composition of these cosmic rays. It is an effective method to test and verify the radiation damage of electronic components in space with high-energy proton beams. According to the statistics of Particle Therapy Co-Operative Group (PTCOG) as of December 2020 [1], there are several proton therapy facilities in operation or planned in Taiwan, and these facilities are anticipated to not only treat cancer but also provide beam services to the industry or academia.
Taiwan is a small island, which is highly populated. Most of these proton therapy facilities are located in areas with high population density, radiation shielding design and dose assessment have become important issues. In the initial design stage of the proton therapy facilities, multiple changes to the shielding design are predictable. Therefore, the simplified approach based on the point-source line-of-sight approximation is friendly because it is intuitive and easy to use. In principle, by selecting shielding parameters according to the problem, the shielding thickness of any wall or the transmission dose rate at any location outside the shield can be quickly estimated. In the final design stage of the facility, Agosteo [2] suggested the use of accurate but time-consuming Monte Carlo simulation for double-checks.
During the proton beam services, the excess proton beam will be directed to the beam dump. In the radiation shielding design, it is considered an important beam loss point. The simplified approach is one of the options [3] to quickly assess the dose around the facility, which considers the inverse-square law of distance and the exponential attenuation of radiation in a shield. The application of the simplified approach in single-layer and double-layer shielding are well known [4, 5], while the three-layer or more is unclear. This case is a three-layer combination, including the double-layer shielding (iron and polymethyl methacrylate [PMMA]) of the beam dump and the concrete wall of the room. Based on the concept of double-layer shielding, the authors intend to extend the concept to this. The shielding parameters of the PMMA shielding material were rare in the literature. If the simplified approach was used to do the shielding design, the prerequisite is to have the corresponding shielding parameters. The purpose of this study is to expand the existing Monte Carlo-based data sets to allow the simplified approach to cover the application of proton beams more widely. At the same time, to demonstrate the effectiveness of the generated data sets, this study emphasizes the consistent comparison between the data sets with the point-source light-of-sight approximation and those acquired by Monte Carlo simulation for dose rate around the laboratory with the therapeutic level proton beam.
Materials and Methods
Based on the experience in establishing shielding parameters [5, 6], three indispensable simulations were used to confirm not only the suitability of the physical model for the generation phase but also the applicability of the shielding parameter database for the practical stage, including neutron yield calculation, Monte Carlo-based data sets generation, and dose assessment of simple shielding design case.
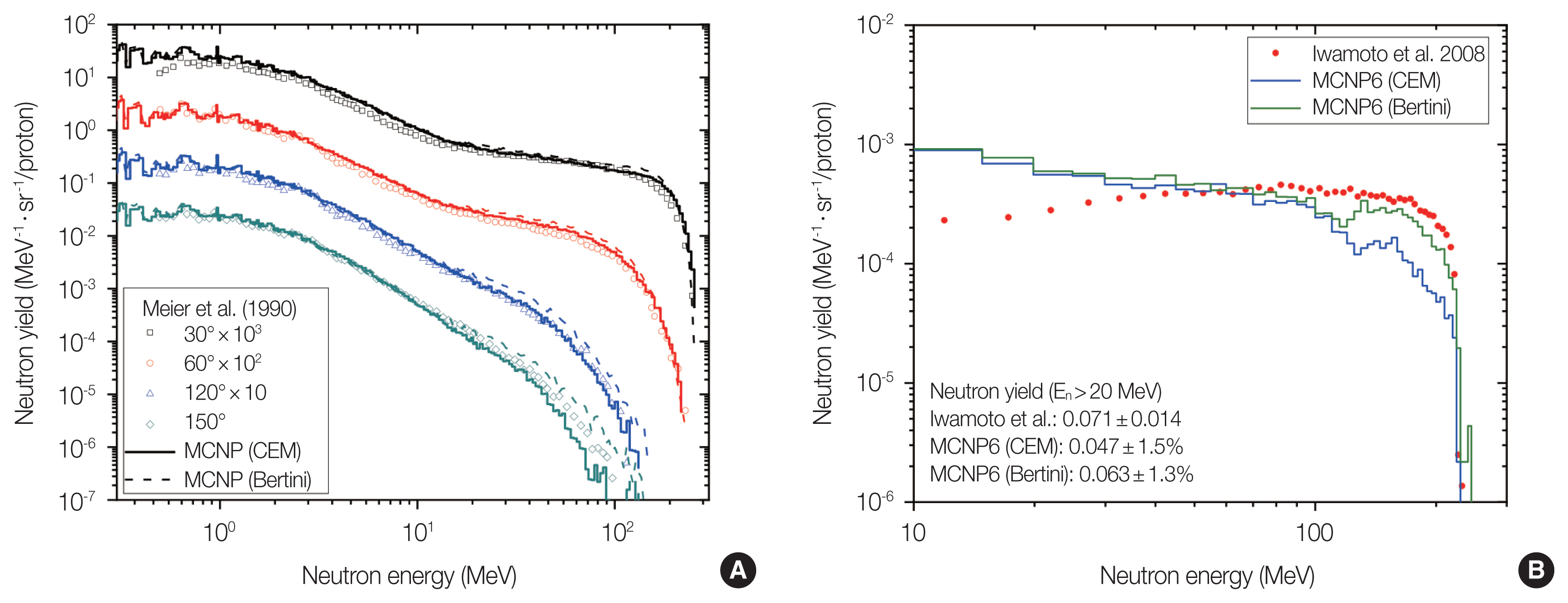
1. Neutron Yield Calculation and Validation
In this study, the literature whose beam energy and target material are close to proton therapy was selected as the target of neutron yield calculation. Not only the experimental results of Meier et al. [7] in 1990 but also the experimental results of Iwamoto et al. [8] in 2008 were used as the validation target for calculating the neutron yield of beam bombardment of high-density targets (such as iron or copper) and low-density targets (such as tissue or graphite). The time-of-flight technique is adopted in the two references. In the experiment of Meier et al. [7], the configuration of the experiment is that a 256 MeV proton beam bombards an iron target. The thickness and radius of the target are both 8 cm. The neutron yield is measured at the position of 30°, 60°, 120°, 150° with the beam direction. In the experiment of Iwamoto et al. [8], the configuration of the experiment is that a 250 MeV proton beam bombards a graphite target. The thickness and radius of the target are both 27.5 cm. The neutron yield is measured at the position of the beam direction. In the verification calculation, this study uses MCNP6 [9] to calculate the neutron yield. The ENDF/B-VI (.24c) cross-section data library is used for the neutron; the LA150 (.24h) cross-section data library is used for the proton, and the physics model (ICEM parameter in LCA card) uses the Bertini model (default value of MCNPX) and the CEM model (default value of MCNP6) to observe whose calculation result is close to the experiment to select as a physical model for subsequent calculations. Fig. 1 shows the comparison of experimental measurements and Monte Carlo calculations, including beams bombarding high-density and low-density target materials. In Fig. 1, the calculation results of the Bertini model are reasonably consistent with the measurement in a large range. Therefore, the Bertini model was selected for subsequent calculations unless specified otherwise.
2. Monte Carlo-based Data Sets Generation
This study uses the MCNP6 Monte Carlo code based on the pointwise cross-section library as a tool to calculate the depth dose distribution or dose attenuation curve of a series of beam/target/shield combinations. The data is fitted by using Equation (1) to generate shielding parameters for the source terms and the attenuation lengths.
In Equation (1)H is the ambient dose equivalent (H*(10)) outside the shield along the θ direction (in Sv); d is the shield thickness (in g/cm2); r is the shortest distance between the source and the evaluation point (in m); H0 and λ are the source terms and the attenuation lengths. The units of H0 and λ are Sv·m2/proton and g/cm2, respectively.
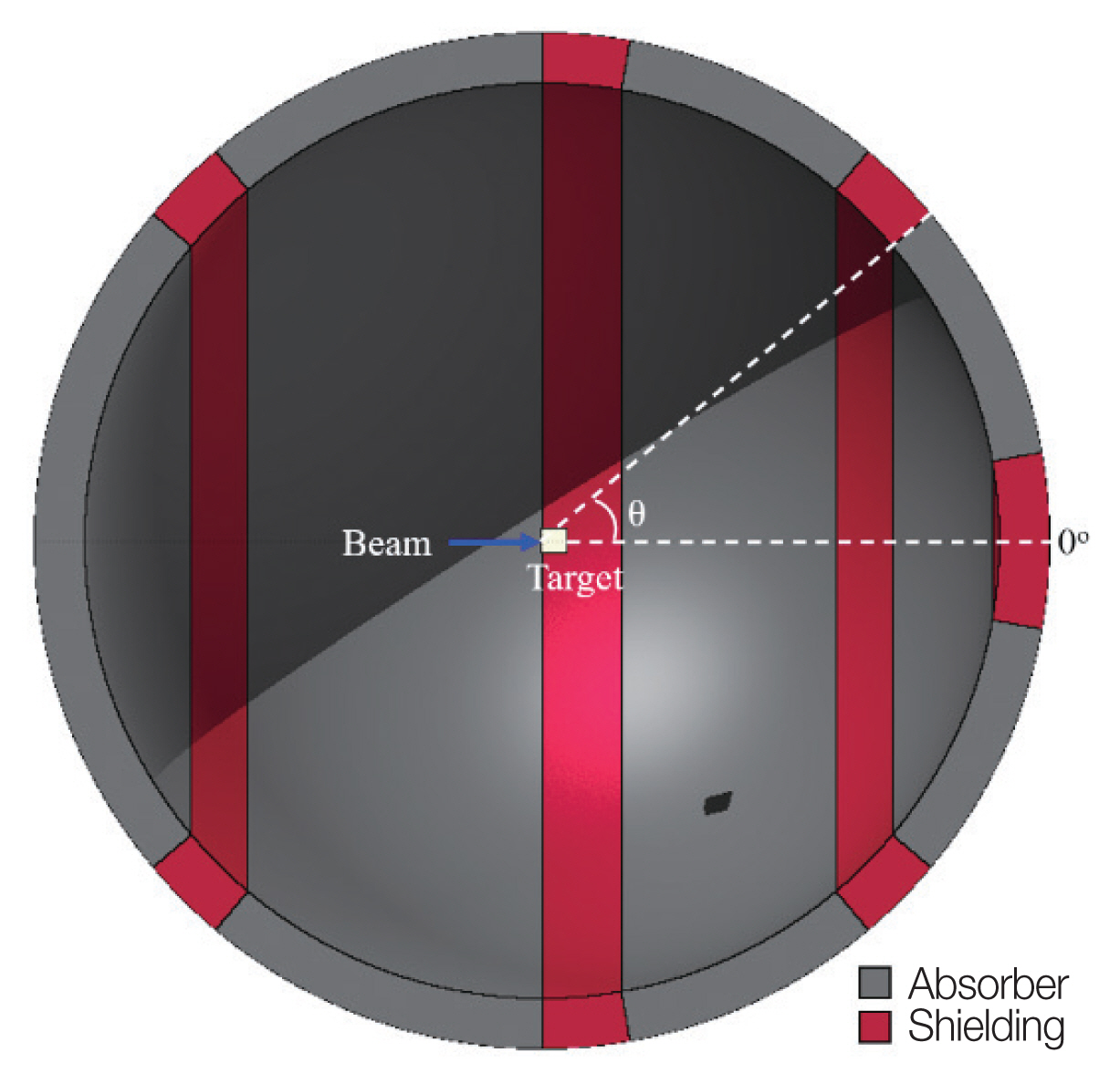
Fig. 2 shows a schematic diagram of the deep-penetration transport model for calculating the dose attenuation curve of a series of beam/target/shield configurations. In the deep-penetration transport calculation, the radiation sources are 100, 150, 200, 250, and 300 MeV proton beams, respectively. The geometry of the target is a right cylinder, that is, the thickness and diameter of the target are the same. In this study, tissue, graphite, iron, and copper were considered as the target material, and the densities of the targets are 1.0, 2.253, 7.87, and 8.96 g/cm3, respectively. Depending on the proton energy, the thicknesses of the tissue targets are 9, 18, 29, 42, and 56 cm; the thicknesses of the graphite targets are 6, 11, 19, 25, and 34 cm; the thicknesses of the iron and copper targets are 1.5, 3, 5, 7, and 9.5 cm. In the geometry and material configurations, a hollow spherical shell with an inner radius of 9,000 cm and a thickness of 600 cm is adopted. The shell material is PMMA with a density of 0.94 g/cm3. Not only the primary beam (proton) but also the secondary particles (protons, neutrons, photons, and electrons) produced by the primary beam with the target and shell are tracked in a simplified shielding model, as shown in Fig. 2. Fig. 2 is a three-dimensional schematic diagram, the component includes a target and a hollow spherical shell. The spherical shell was divided into red and gray regions. Once the particle enters the spherical shell, the program will continue to track the particle when the particle enters the red region, on the contrary, the program stops tracking particles. Regarding the interaction of the radiation and the matter, this study uses a pointwise cross-section library, namely ENDF/B-VI, and a built-in nuclear reaction physics model. The ENDF/B-VI (.24c) is used for neutron; the ENDF/B-VI.8 (.84p) and e103 (.03e) are used for photon and electron respectively; the LA150 (.24h) is used for proton. The cutoff energy of photon and electron is 100 keV. In this study, H*(10) was used as the dose index unless specified otherwise, and the unit is Sievert (Sv). Regarding the scorings, the surface flux (F2) tally is used to score protons, neutrons, photons, and electron fluence, and the fluence to dose conversion factor of the International Commission on Radiological Protection (ICRP) Report 74 [10] and Pelliccioni [11] were applied to obtain the H*(10). A variance reduction technique called the IMP cell importance based on geometric splitting and Russian roulette in MCNP is adopted to overcome the deep-penetration problem.
3. Dose Assessment around the Laboratory
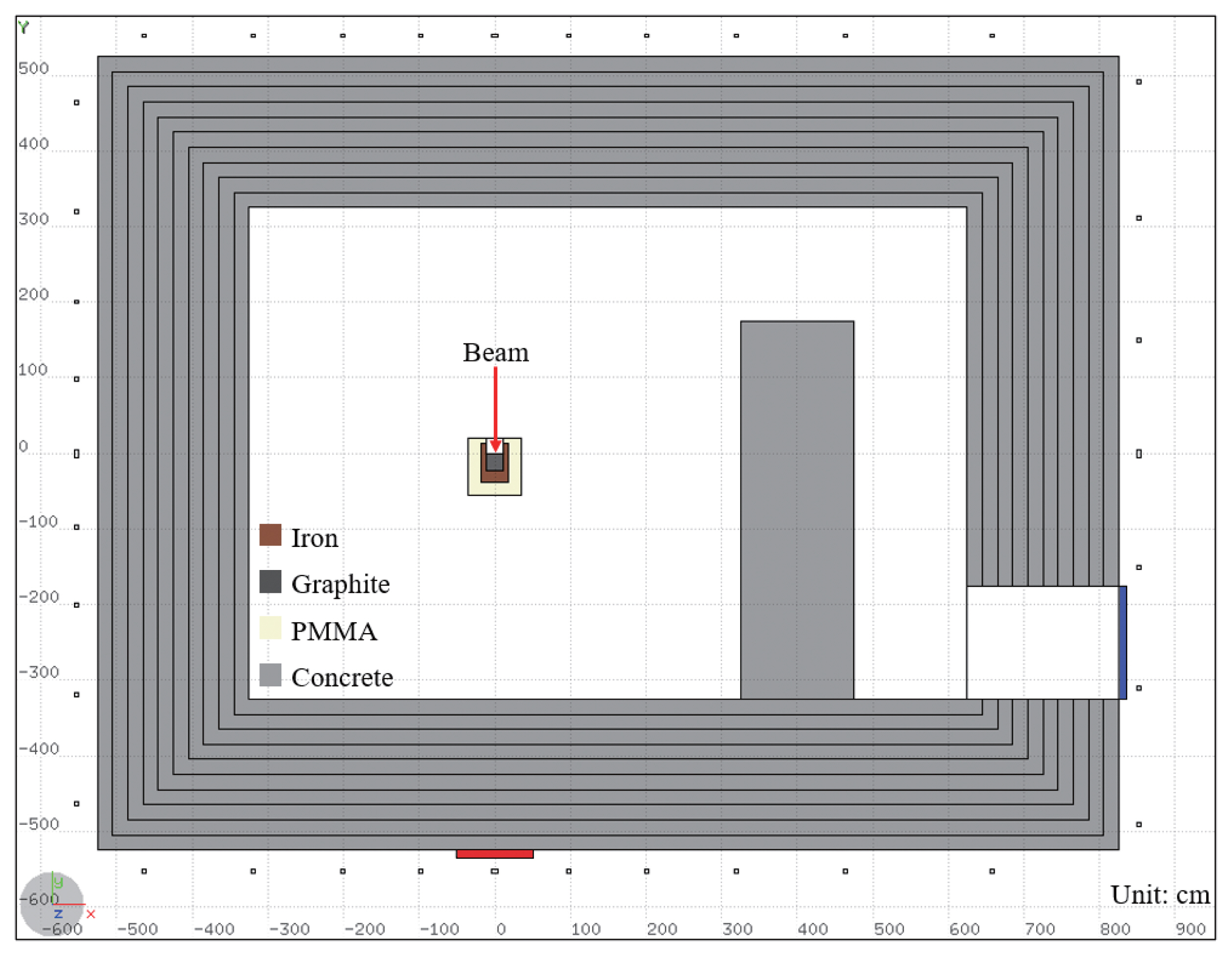
Fig. 3 shows the configuration of a hypothetical proton beam irradiation laboratory (hereinafter referred to as the laboratory) drawn by the flair software [12], including an indoor space of 650×650×300 cm3 and a three-leg labyrinth design, the thickness of the labyrinth wall is 150 cm, and the shielding thickness is assumed to be 200 cm of concrete. Thirty-six detectors are installed outside the laboratory for evaluating the dose rate, and two detectors are installed in the direction of the proton beam direction (red) and the labyrinth entrance (blue) for observing the neutron spectra.
In this study, MCNP6 was used to simulate the radiation transport calculation of the aforementioned laboratory, and the results will be used as the reference for comparison of the simplified approach. In the transport calculation, the radiation source is a 250 MeV proton beam, which directly bombards the beam dump located in the center of the laboratory. The composition of the beam dump includes graphite, iron, and PMMA. The parameter setting of the transport calculation is consistent with those in the shielding parameter generation. The results include dose rates outside the laboratory and neutron spectra at proton beam direction outside the room (red) and labyrinth entrance (blue).
According to the principle of shielding parameter production, (H1, λ1) and (H2, λ2) are the shielding parameters obtained from the curve fitting of the depth dose in the shallow and deep regions [5, 6], respectively. Therefore, in practice, it is recommended to use (H1, λ1) to evaluate the shallow dose of PMMA and concrete with a shielding thickness of less than 150 cm or iron and lead with a shielding thickness of less than 75 cm, otherwise, (H2, λ2) was recommended to use to evaluate the deep dose. Based on the shielding design in Fig. 3 and the principle of using shielding parameters, this study uses the Equation (1) with the Monte Carlo-based data sets to evaluate the dose at 36 detectors outside the shielding.
Results and Discussion
1. Database of Shielding Parameters
Fig. 4 shows the dose attenuation curve and fitting results of the PMMA shielded by the 250 MeV proton beam bombarding the graphite target. In the figure, the secondary particles penetrate the PMMA shield, the slope of the dose attenuation is divided into three sections. The first section has a thickness between 0 to 40 cm, the second section has a thickness between 40 to 150 cm, and the third section has a thickness of over 150 cm. According to the depth dose distribution in Fig. 4, the second and third sections are adopted as the shallow and deep shielding fitting ranges to obtain the corresponding shielding parameters.
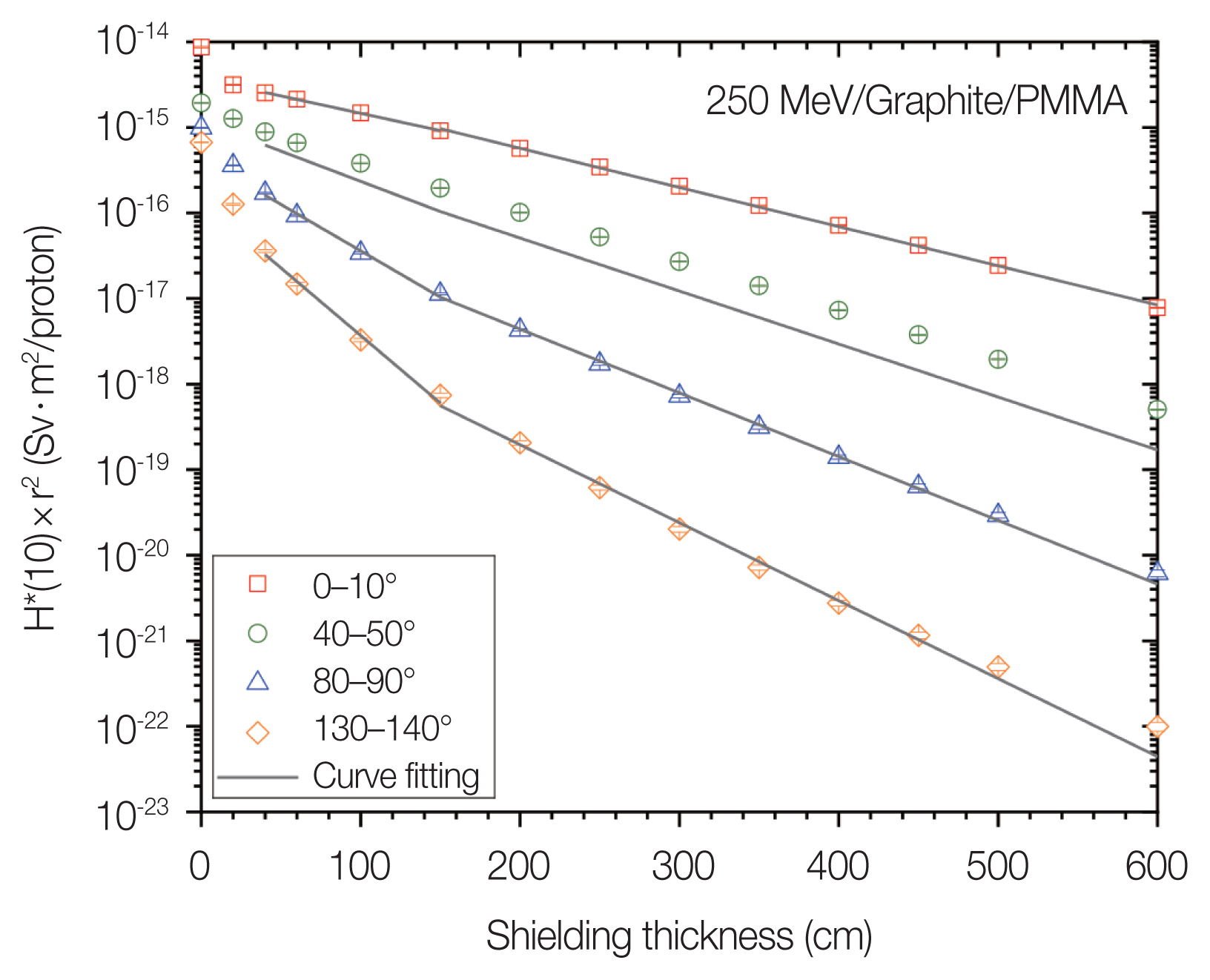
Dose attenuation curve of 250 MeV proton beam bombarding a graphite target with polymethyl methacrylate (PMMA) shielding.
Fig. 5 shows the Monte Carlo-based data sets such as the source terms and the attenuation lengths of the PMMA, concrete, iron, and lead shielding of a 250 MeV proton beam bombarding a graphite target, and they are also the shielding parameter selected for the dose assessment. For each beam/target/shield combination, the angular distribution of shielding parameters is related to the angular distribution of secondary neutrons. The secondary neutrons generated by the proton beam bombarding the target have higher energy and intensity at the beam direction than others. Therefore, the angular distribution of shielding parameters shows a tendency to attenuate as the angle increases. If the shielding material is considered as a variable, the shielding parameters of different shielding materials are also different, which is related to the neutron spectrum characteristics in the shield. PMMA cannot effectively attenuate the high-energy neutrons (En>10 MeV), but it is an effective shielding material for fast neutrons (0.1 MeV<En<10 MeV). Although iron and lead can effectively attenuate high-energy neutrons, the attenuation capacity is poor for fast neutrons; the attenuation of high-energy neutrons by concrete is not as effective as iron and lead, but it is better than PMMA. Otherwise, the attenuation capacity for low-energy neutrons is not as good as PMMA, but better than iron and lead.
2. Characteristics of the Radiation Field
Fig. 6A shows the beam-level dose distribution of secondary particles (including neutrons and photons) by using MCNP6 to calculate the radiation source of 250 MeV proton beam to bombard the beam dump located in the center of the laboratory. This study uses an Intel Core i9-9980XE CPU 3.0 GHz (18 cores/36 threads), the memory capacity of 64 GB, and Windows 10 operating system on a personal desktop computer to perform this calculation. It took 31 threads to complete the simulation in 5 days. In Fig. 6, the dose ranges from 10−8 to 10−18 μSv/proton, which from the proton beam loss point at the beam dump in the center of the laboratory to the outdoor covers about 10 orders of magnitude attenuation. Outside the laboratory, the position with the highest dose is approximately 10−11 μSv/proton in the beam direction, and the position with the lowest dose is approximately 10−18 μSv/proton in the upper right corner of the laboratory.
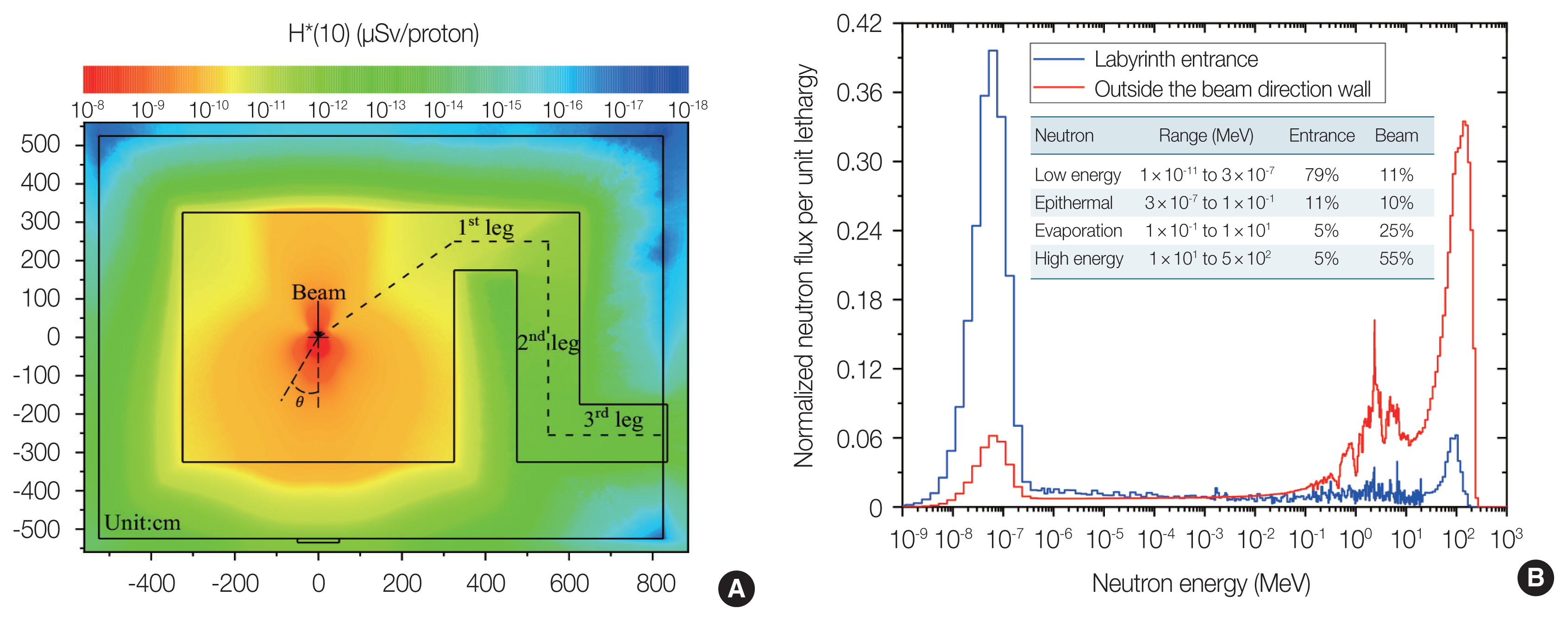
The dose rate distribution of laboratory (A), the neutron spectra outside the beam direction wall, and labyrinth entrance (B).
Fig. 6B shows the calculated neutron spectra outside the beam direction wall and at the labyrinth entrance. The neutron spectrum at the entrance of the labyrinth is based on the low-energy neutrons (76%) after continuous scattering and reflection of neutrons in the labyrinth and the high-energy neutrons (5%) with an energy of about 100 MeV. The neutron spectrum outside the beam direction wall is completely different from the former. The energy spectrum shows three significant peaks, namely low-energy neutrons (12%), fast neutrons with an energy of about 1 MeV (24%), and high-energy neutrons (53%) with an energy of about 100 MeV.
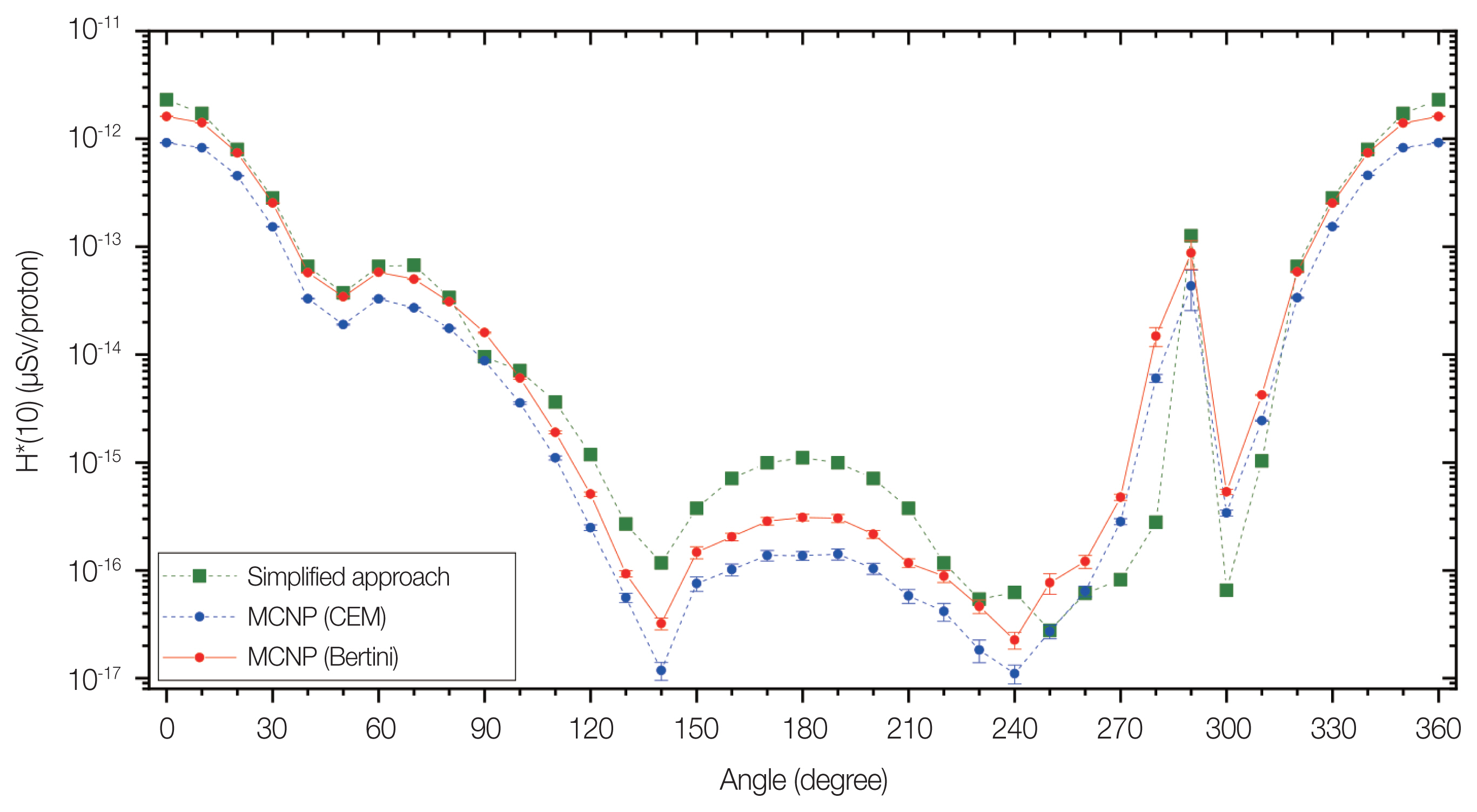
3. Comparison of a Simplified Approach and Monte Carlo Method in Dose Assessment of Simple Shielding Design Case
Regarding the time spent on dose assessment around the facility, the simplified approach takes 2 hours to complete, while the direct Monte Carlo simulation takes 8 hours (equivalent to 1 working day) for modeling and debugging, and 120 hours for transport calculation, which can be solved through parallel calculation. If the transport calculation time is not taken into account, the Monte Carlo simulation is four times that of the simplified method. Fig. 7 shows the use of a simplified approach and direct Monte Carlo simulation for dose assessment in 36 locations around the laboratory. In the consistency comparison of the results, the ratio between the simplified approach and the MCNP6 with the Bertini model is between 1 and 1.5 in the range of 0°–60°, and the ratio of the two is between 0.6 and 2.4 in the range of 70°–120°. In 130°–180°, the ratio of the two is between 2.5 and 3.7. Close to the labyrinth entrance, the ratio of the two is about 0.1. Compared with MCNP6 using the CEM model, in 0°–60°, the ratio is between 1.7 and 2.5, and in 70°–120°, the ratio of the two is between 1.1 and 4.8. In 130°–180°, the ratio of the two is between 4.8 and 10. Close to the labyrinth entrance, the ratio of the two is about 0.2. It is shown that selecting the appropriate shielding parameters for the problem can quickly and conservatively obtain the transmitted dose rates outside the laboratory, and these doses are consistent with the results of MCNP in a large range. The doses near the labyrinth entrance were underestimated by the simplified approach. This is inevitable because the dose at the entrance of the labyrinth consists of the radiation transmitted part and the radiation streaming part. In this regard, the Monte Carlo-based source terms can be used in estimating the doses along the labyrinth by a proper coupling with semi-empirical formulae that parameterize the behavior of neutrons streaming through labyrinths.
Conclusion
Radiation shielding is an important issue for those proton therapy facilities located in densely populated areas. Monte Carlo simulation is the most accurate method, but it is not practical in the preliminary design of the facility. The simplified approach based on the point-source light-of-sight approximation would be a good choice at this stage. The principle of using the simplified approach is to select the appropriate target material, shielding material, and proton beam energy. This study has expanded the existing Monte Carlo-based data set to allow the simplified approach to be used for dose assessment or radiation shielding design for beam services in proton therapy facilities. The data sets related to the beam dump are added. The energy range of the proton beam contained in the database is from 100 to 300 MeV, the target material covers tissue, graphite, iron, and copper, and the shielding material covers PMMA, concrete, iron, and lead. This study proves that the Monte Carlo-based data sets are reliable through the following steps. The first step is to validate the physical model used to generate the data sets by neutron yield. The second step is that the data sets are used to evaluate dose rates and compare them with the accurate Monte Carlo method. Besides, it should be noted that the default model of the MCNP6 is no longer the Bertini model but the CEM model, therefore, the results of the simplified approach will be more conservative when it was used to do the double confirmation of the final shielding design.
Acknowledgements
This research was funded by the Radiation Protection Association R.O.C.
Notes
Conflict of Interest
No potential conflict of interest relevant to this article was reported.
Author Contribution
Conceptualization: Lai BL, Sheu RJ. Funding acquisition: Chang SL. Investigation and methodology: Lai BL, Sheu RJ. Writing of the original draft: Lai BL. Writing of the review and editing: Lai BL, Chang SL. All the authors have proofread the final version.