AbstractBackgroundThis study aims to determine the effective atomic number (Zeff) from dual-energy image sets obtained using a conventional computed tomography (CT) simulator. The estimated Zeff can be used for deriving the stopping power and material decomposition of CT images, thereby improving dose calculations in radiation therapy.
Materials and MethodsAn electron-density phantom was scanned using Philips Brilliance CT Big Bore at 80 and 140 kVp. The estimated Zeff values were compared with those obtained using the calibration phantom by applying the Rutherford, Schneider, and Joshi methods. The fitting parameters were optimized using the nonlinear least squares regression algorithm. The fitting curve and mass attenuation data were obtained from the National Institute of Standards and Technology. The fitting parameters obtained from stopping power and material decomposition of CT images, were validated by estimating the residual errors between the reference and calculated Zeff values. Next, the calculation accuracy of Zeff was evaluated by comparing the calculated values with the reference Zeff values of insert plugs. The exposure levels of patients under additional CT scanning at 80, 120, and 140 kVp were evaluated by measuring the weighted CT dose index (CTDIw).
Results and DiscussionThe residual errors of the fitting parameters were lower than 2%. The best and worst Zeff values were obtained using the Schneider and Joshi methods, respectively. The maximum differences between the reference and calculated values were 11.3% (for lung during inhalation), 4.7% (for adipose tissue), and 9.8% (for lung during inhalation) when applying the Rutherford, Schneider, and Joshi methods, respectively. Under dual-energy scanning (80 and 140 kVp), the patient exposure level was approximately twice that in general single-energy scanning (120 kVp).
IntroductionParticle therapy has become a major part of radiation therapy (RT) owing to its physical benefits. The kinetic energy of the particles is almost deposited distal to their tracks. Therefore, the target volume has a high conformal dose distribution, which effectively spares normal tissue from radiation exposure. In particle therapy, the stopping power ratio (SPR) is significant for dose calculations [1]. The planning target volume (PTV) margin includes the uncertainty determined based on the SPR. Therefore, the uncertainty of the SPR should be minimized to improve the clinical benefit of particle therapy [2].
In particle therapy, a single-energy computed tomography (SECT) image is generally used to generate a treatment plan for delineation and dose calculation. The SPR is estimated from a piecewise linear fit between the Hounsfield unit (HU) and SPRs, and data for human organs or measurements of phantoms consisting of tissue substitutes have been published [3]. However, additional margins (e.g., 3.5 mm for protons) of the absolute particle range are needed clinically in the distal direction to account for the limit of the correlation between photon attenuation coefficients, proton stopping power, and computed tomography (CT)-related uncertainties [4].
Dual-energy CT (DECT) has been introduce in radiotherapy. For radiation treatment, new methods based on DECT imaging are proposed to improve the quality of radiation treatment [5]. DECT achieves advanced material differentiation by using high and low energy X-ray spectra. The material-specific imaging methods of DECT have been used for several imaging analyses (e.g., monochromatic imaging, effective atomic number mapping, virtual non-contrast or unenhanced imaging, iodine mapping, automatic bone removal, and lung vessel analysis) [6]. Furthermore, DECT can provide the effective atomic number (Zeff) and electron density [5]. The SPR can be derived from the effective atomic number (Zeff) and electron density. The Zeff is converted to mean excitation potential. SPR can be calculated using electron density and mean excitation potential according to Bethe-Bloch equation [7]. When DECT is applied, the accuracy of the SPR can be within 1%–2% [7, 8]. Based on a comparison of range calculations based on SECT/DECT scanning, the range differences were 1 and 4.1 mm for the brain and prostate, respectively [9].
However, DECT for RT simulations has not yet been developed. Diagnostic DECT scanners has some restrictions on use for RT. The maximum bore size is 70 cm among commercially available diagnostic DECT scanners. There are some restrictions on RT. For an RT simulation, the bore size must be larger when using an immobilizer to maintain the patient’s position. In addition, it is costly to maintain additional DECT equipment at an RT clinic.
A conventional CT simulator that employs single-energy scanning can change the tube energy per scan, but it cannot perform dual-energy scans simultaneously. For example, for each scan, a commercial CT simulator can use only one of three different energies—i.e., 80, 120, and 140 kVp [10]. The dual-energy image set can be obtained through double scanning using two different diagnostic X-ray energies. The effective atomic number and electron density can be calculated from a dual-energy image set [11]. Finally, the SPR can be estimated from these data. In this study, we determined the effective atomic number (Zeff) using a conventional CT simulator (CT-sim) based on SECT. The calculated Zeff of a representative set of materials was evaluated by comparing our results with known chemical compositions and densities, which served as reference values. To obtain the low and high energy image sets, additional scanning should be performed. The weight CT dose index (CTDIW) was measured for three tube currents to evaluate the additional exposure to the patient.
Material and Methods1. CT, Reference Phantom, and Image ProcessingThe dual-energy image sets were obtained with Brilliance CT Big Bore (BBB; Philips, Cleveland, OH, USA) which includes three tube potentials: 80, 120, and 140 kVp. BBB is a dedicated CT simulator for RT with an 85 cm bore size and a flat bed.
An electron density phantom (CIRS Model 062M; CIRS Inc., Norfolk, VA, USA) was scanned using BBB. Fig. 1A shows the scan setup. The phantom consists of a water-equivalent material disk and tissue-equivalent plugs (Table 1). Fig. 1B shows the arrangement of the insert plugs on the disk. The mass density and chemical composition were obtained from the literature [10, 12].
The electron density phantom was sequentially scanned using tube potentials of 80 and 140 kVp. A set of CT images was bilaterally filtered for edge-preserving noise reduction, and equations were solved for each voxel.
2. Reference Calculation of the Electron Density (ED, re) and ZeffZeff was calculated according to Equation (1), and fi, the fraction of total number of electrons associated with each element, was calculated according to Equation (2) [12]:
In this study, the value of nz was selected as 2.94 for the Philips method in accordance with the Mayneord formula and other publications [13].
The Zeff were derived from the low- and high-energy data. The compositions and densities (physical and electron) of the tissues were obtained from data published by the National Institute of Standards and Technology (NIST). The energy-dependent attenuation curve was plotted by referring to NIST elemental attenuation values. The created curve was fitted to match the reference value of the DE image set. To find the best fitting curve comparing the value of literature tissues, the two parameters related to linear combination coefficients was adjusted.
3. Estimation of Zeff from the DE Image SetZeff was estimated via three different methods. Regarding the method suggested by Rutherford et al. [14], Zeff was calculated as follows:
where HUL and HUH are CT numbers at low and high energies, respectively, and A, B, C, and m are fitting parameters. The MATLAB optimization toolbox (R2015b; MathWorks Inc., Natick, MA, USA) was used to fit the parameters.
Regarding the second method, Zeff was calculated via Schneider stoichiometric calibration as follows [15]:
(4)where Zw is the effective atomic number of water. ki,L, ki, and H are fitting parameters. The fitting parameters were determined using the MATLAB optimization toolbox as in the first method.
Third, Zeff was calculated using the Joshi method [16]. In this method, Zeff is estimated based on the ratio of low to high energy attenuation coefficients. The energy attenuations coefficients were calculated using the data provided by NIST. The basis material images were generated by a tungsten anode spectral model using interpolating polynomials (TASMIP) [17]. The effective linear attenuation coefficients of the high and low energies were calculated using the attenuation data. The basis material (decomposition) image can be expressed for the dependency of the basis material combination. Finally, a monochromatic energy image can be derived using the attenuation data. When the pixel value of the image has a monochromatic attenuation ratio, Zeff can be expressed in terms of the monochromatic attenuation ratio because of the energy independence of the ratio. To calculate Zeff, the ratio of Zeff to the attenuation coefficient was plotted using a polynomial fit. Consequently, the monochromatic image was converted to Zeff by plotting. Fig. 2 shows the workflow of Zeff estimation for the Joshi method.
4. CTDI MeasurementFor the CTDI measurement, head and body CTDI phantoms (Model 76-414-4150NAD; Fluke Corp., Everett, WA, USA) were used with an X-ray CT detector (Unfors RaySafe AB, Billdal, Sweden) and a black piranha quality assurance (QA) meter (RTI Electronics AB, Moelndal, Sweden). The CTDIw was calculated as follows:
where CTDI100 is 100 mm active chamber length, and D(z) is the dose profile along the Z-axis. CTDIctr and CTDIperi stand for the center and peripheral chamber locations, respectively. CTDIperi was measured at four holes (12-, 3-, 6-, and 9-hour holes within the perimeter).
Results and DiscussionRegarding the fitting parameters of the first method, A is 2.73×10−4, B is 1.08, C is 3.85×10−5, and m is 3.88. The photoelectric term at high energy is considered negligible because the cross section is extremely low at 140 kVp. Through the repeated fitting procedure, the standard deviation and R2 were identically obtained as applied to the reference phantom.
The spectral parameters of the second method are shown in Table 2. The values were derived via the nonlinear least squares regression of Equation (2). The calculation was performed based on the composition and density of the reference phantom. The parameters derived based on regression were validated via comparison with the inserts of the reference phantom.
Fig. 3 shows the function curve for the third method. The image sets obtained at low (80 kVp) and high (140 kVp) energies were converted into water and bone material images. Each converted image was extracted as two (80 and 140 keV) virtual monochromatic images (VMIs). Zeff was calculated using the VMIs and function curve.
The Zeff values of the insert plug calculated using the three different methods are listed in Table 3. Fig. 4 shows the calculated Zeff parametric map for the three different methods. The second method achieves the best estimation. The estimations for the high-Zeff material (i.e., bone material) are poor. The Zeff of the lung has the largest difference among the results of all the methods.
Although denoising was performed to reduce the standard deviation, the image still contained noise. Despite the same material in the insert plug, the value of Zeff in the circle has a large deviation on the image. Further, streak artifacts from high-attenuation objects can be observed. These artifacts, which primarily arise from the bone plug, affect the pixels corresponding to other plugs. Therefore, the image noise increases. To minimize the position-related artifacts, the inserts of phantom might be re-arrangement randomly. To reduce the image noise, the techniques for removal or reduction of noise should applied such as Gaussian or median filter.
In this study, Zeff estimation was performed under several approximations and assumptions. The main assumption was that HU and Zeff have a direct relationship that can be expressed by a mathematical equation and fitting curve. Therefore, the accuracy of the Zeff matrix is determined by the noise level of the base image. The inconsistency between the estimations and actual values affects the applicability of this method in clinical applications, such as SPR calculation. Therefore, improved imaging de-noising algorithm should be applied maintaining the image quality.
The CTDIw values for three different tube potentials (90, 120, and 140 kVp) are presented in Table 4. In this study, CT scanning was performed twice to obtain a dual-energy image set by changing the tube current. Two repeated scans were required to acquire a dual-energy image using CT-sim. Therefore, additional exposure was expected. In general, a 120-kVp tube potential is used for patient scanning. If 80 and 140 kVp are used for dual-energy scanning, the level of patient exposure will approximately double in comparison with 120 kVp single scan.
ConclusionDECT can be employed to estimate Zeff by processing dual CT images obtained with different X-ray energies. Zeff is an essential factor for calculating the SPR. To date, no commercial DECT-sim for RT has been reported. In this study, Zeff was calculated from two image sets scanned via conventional SECT-sim using three different methods. The feasibility of Zeff calculation based on SECT was evaluated. To improve the calculation accuracy, an image noise and artifact reduction method is required.
NotesAuthor Contribution Conceptualization: Choi CH. Data curation: Kim B, Choi CH. Formal analysis: Kim B, Choi CH. Funding acquisition: Park JM, Choi CH. Methodology: Jung S, Kim B. Visualization: Jung S. Writing - review & editing: Kim J, Choi CH. Investigation: Kim B, Kim J. Resources: Kim J. Validation: Park JM. AcknowledgementsThis work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (No. NRF-2019M2A2B4095126).
References1. Yang M, Zhu XR, Park PC, Titt U, Mohan R, Virshup G, et al. Comprehensive analysis of proton range uncertainties related to patient stopping-power-ratio estimation using the stoichiometric calibration. Phys Med Biol. 2012;57:4095-4115.
2. Li B, Lee HC, Duan X, Shen C, Zhou L, Jia X, et al. Comprehensive analysis of proton range uncertainties related to stopping-power-ratio estimation using dual-energy CT imaging. Phys Med Biol. 2017;62:7056-7074.
3. Hudobivnik N, Schwarz F, Johnson T, Agolli L, Dedes G, Tessonnier T, et al. Comparison of proton therapy treatment planning for head tumors with a pencil beam algorithm on dual and single energy CT images. Med Phys. 2016;43:495.
4. Bourque AE, Carrier JF, Bouchard H. A stoichiometric calibration method for dual energy computed tomography. Phys Med Biol. 2014;59:2059-2088.
5. Landry G, Seco J, Gaudreault M, Verhaegen F. Deriving effective atomic numbers from DECT based on a parameterization of the ratio of high and low linear attenuation coefficients. Phys Med Biol. 2013;58:6851-6866.
6. Goo HW, Goo JM. Dual-energy CT: new horizon in medical imaging. Korean J Radiol. 2017;18:555-569.
7. Farace P. Experimental verification of ion stopping power prediction from dual energy CT data in tissue surrogates. Phys Med Biol. 2014;59:7081-7084.
8. Hunemohr N, Krauss B, Tremmel C, Ackermann B, Jakel O, Greilich S. Experimental verification of ion stopping power prediction from dual energy CT data in tissue surrogates. Phys Med Biol. 2014;59:83-96.
9. Wohlfahrt P, Mohler C, Stutzer K, Greilich S, Richter C. Dual-energy CT based proton range prediction in head and pelvic tumor patients. Radiother Oncol. 2017;125:526-533.
10. Zhu J, Penfold SN. Dosimetric comparison of stopping power calibration with dual-energy CT and single-energy CT in proton therapy treatment planning. Med Phys. 2016;43:2845-2854.
11. Garcia LI, Azorin JF, Almansa JF. A new method to measure electron density and effective atomic number using dual-energy CT images. Phys Med Biol. 2016;61:265-279.
12. Hua CH, Shapira N, Merchant TE, Klahr P, Yagil Y. Accuracy of electron density, effective atomic number, and iodine concentration determination with a dual-layer dual-energy computed tomography system. Med Phys. 2018;45:2486-2497.
13. Mayneord WV. The significance of the roentgen. Acta Int Union Against Cancer. 1937;2:271-282.
14. Rutherford RA, Pullan BR, Isherwood I. Measurement of effective atomic number and electron density using an EMI scanner. Neuroradiology. 1976;11:15-21.
15. Schneider W, Bortfeld T, Schlegel W. Correlation between CT numbers and tissue parameters needed for Monte Carlo simulations of clinical dose distributions. Phys Med Biol. 2000;45:459-478.
Fig. 1(A) Electron density phantom scanning setup with the Big Bore CT simulator. (B) Phantoms and insert arrangements for measurement of the accuracy of the Zeff estimation. CT, computed tomography. 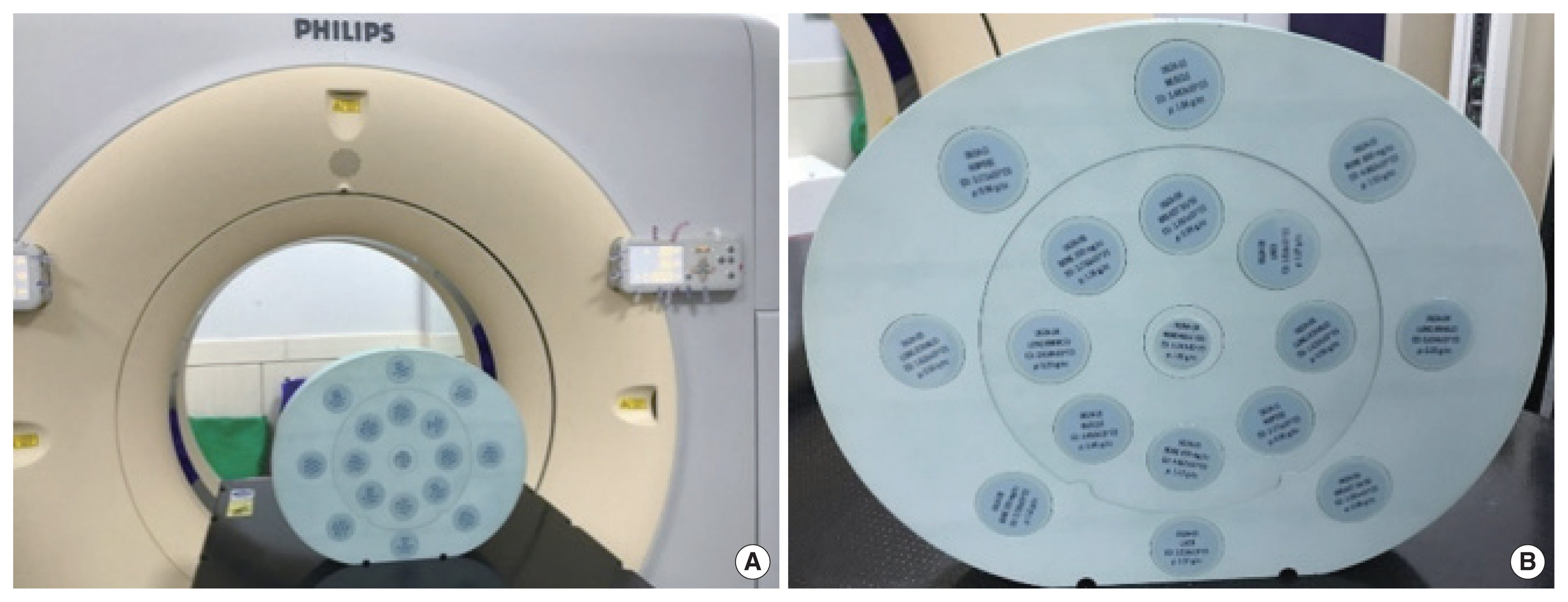
Fig. 2Flow chart of the Philips Zeff estimation method, which is based on image-based material decomposition. CT, computed tomography; TASMIP, tungsten anode spectral model using interpolating polynomials; NIST, National Institute of Standards and Technology. 
Table 1Physical Density, ED, and RED for the Insert Plug of the Phantom Table 2Spectral Parameters k1 and k2 of the 80 and 140 kVp X-ray Beams
Table 3Zeff Values and the Relative Differences between Estimated Values and Theoretical Values |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||