Monte Carlo Calculation for Production Cross-Sections of Projectile’s Isotopes from Therapeutic Carbon and Helium Ion Beams in Different Materials

Quazi Muhammad Rashed Nizam; Asif Ahmed; Iftekhar Ahmed

doi:10.14407/jrpr.2023.00262

J. Radiat. Prot. Res > Volume 48(4); 2023 > Article

Nizam, Ahmed, and Ahmed: Monte Carlo Calculation for Production Cross-Sections of Projectile’s Isotopes from Therapeutic Carbon and Helium Ion Beams in Different Materials

Original Research

Journal of Radiation Protection and Research 2023; 48(4): 204-212.

Published online: December 31, 2023

DOI: https://doi.org/10.14407/jrpr.2023.00262

Monte Carlo Calculation for Production Cross-Sections of Projectile’s Isotopes from Therapeutic Carbon and Helium Ion Beams in Different Materials

Quazi Muhammad Rashed Nizam

, Asif Ahmed

, Iftekhar Ahmed

Department of Physics, University of Chittagong, Chittagong, Bangladesh

Corresponding author: Quazi Muhammad Rashed Nizam, Department of Physics, Faculty of Science, University of Chittagong, Chittagong 4331, Bangladesh, E-mail: rnizam.physics@cu.ac.bd

Received July 22, 2023 Revised October 22, 2023 Accepted November 7, 2023

This is an open-access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by-nc/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Background

Isotopes of the projectile may be produced along the beam path during the irradiation of a target by a heavy ion due to inelastic interactions with the media. This study analyzed the production cross-section of carbon (C) and Helium (He) projectile’s isotopes resulting from the interactions of these beams with different materials along the beam path.

Materials and Methods

In this study, we transport C and He ion beams through different materials. This transportation was made by the Monte Carlo simulation. Particle and Heavy Ion Transport code System (PHITS) has been used for this calculation.

Results and Discussion

It has been found that ¹⁰C, ¹¹C, and ¹³C from the ¹²C ion beam and ³He from the ⁴He ion beam are significant projectile’s isotopes that have higher flux than other isotopes of these projectiles. The ⁴He ion beam has a higher projectile’s isotope production cross-section along the beam path, which adds more impurities to the beam than the ¹²C ion beam. These projectile’s isotopes from both the ¹²C and ⁴He ion beams have higher production cross-sections in hydrogenous materials like water or polyethylene.

Conclusion

It is important to distinguish these projectile’s isotopes from the primary beam particles to obtain a precise and accurate cross-section result by minimizing the error during measurement with a nuclear track detector. This study will show the trend of the production probability of projectile’s isotopes for these ion beams.

Keywords: Projectile’s Isotope, Isotope Production Cross-Section, Monte Carlo, Particle and Heavy Ion Transport Code System

Introduction

Ion beam accelerators play a significant role in medical physics [1], radiation physics, accelerator physics, ion implantation, material science, space radiation [2], and cancer therapy [3]. Therefore, it is of paramount importance to understand the mechanism of the interaction between ions and matter to effectively use the ion beams from an accelerator. The total reaction cross-section is one of the most fundamental quantities for understanding the nucleus–nucleus interaction mechanism. However, the total reaction cross-section is difficult to measure experimentally due to various reaction channels. On the other hand, since most reactions undergo a proton change, the total charge changing cross-section (σ_TCC) is an alternative and effective method to understand the reaction cross-section [4]. σ_TCC measures the probability of changing the charge (proton) of a projectile. It is also important to understand the structure and stability of the nucleus [5] and particle spectrum in a cosmic ray [6]. Many experiments have measured σ_TCC in different interactions since 1970 [7–9]. However, neutron changing cross-sections (¹²C to ⁹C–¹⁵C isotopes) were excluded from this σ_TCC measurement.

To conduct this type of experiment, researchers use both active detectors, such as the Cherenkov detector [10], Si detector, different types of scintillators, position sensitive detectors [7, 8, 11], and time projection chambers [12] and passive detectors, essentially track detectors such as CR-39 [13–18] and nuclear emulsion [19]. Track detectors have been used for ion interaction experiments since 1960s [20–22]. Passive detectors such as CR-39 have certain advantages over active detectors in detecting fragments with a range in ‘μm’ scale, multiple fragments from a single interaction, etc. However, the CR-39 detector has a limitation of low mass resolution [23, 24]. As a result, these detectors cannot differentiate between projectiles and their respective isotopes, which is important for experiments such as σ_TCC measurement. The incapability of these detectors to distinguish projectiles and isotopes of the projectile is one of the main sources of error in the experiment. Therefore, it is important to determine the projectile isotopes that are produced before coming to the target because of the interacting materials in the beam line and those inside the target for beam purity.

We analyzed ¹²C and ⁴He as the main ion beam for cancer therapy in this study. Ion beam contamination due to projectile’s isotopes is one of the major and longstanding experimental issues that must be considered [25], which hinders the measurement. Kozma et al. [26] and Kaki [27] attempted to measure the production cross-section of these projectile’s isotopes for different interactions. This study estimated the production cross-sections of projectile’s isotopes for ¹²C and ⁴He ion beams in different media with the Monte Carlo calculation by Particle and Heavy Ion Transport code System (PHITS) [28]. Recently, the use of ⁴He ion has renewed interest for certain therapeutic conditions due to less lateral scattering than the proton and lower impact of the fragmentation tail than in ¹²C ion irradiation. A clinical trial of ⁴He ion at the Heidelberg Ion-Beam Therapy Center has just started [29]. So, the production cross-section of isotopes from the ⁴He ion beam has also been analyzed in this study.

There are very few experimental data on projectile’s isotope production cross-sections (σ_ipc) measured for different interactions. Therefore, our calculated data and the analysis of the trend of projectile’s isotope production in different target materials in this study could be useful for researchers in this field.

Materials and Methods

In this study, JAERI Quantum Molecular Dynamics 2.0 (JQMD 2) [30] incorporated in PHITS version 3.22 was used to simulate the transport of the ¹²C ion beam, and Liège Intranuclear Cascade model (INCL4.6) [31] has been used for the transportation of ⁴He ion beams inside materials such as scatterer (Ta) with density of 16.6 g/cm³, beam monitors (Al) with density of 2.7 g/cm³, and range shifter (polymethyl methacrylate [PMMA] (C₅O₂H₈)_n) with density of 1.91 g/cm³ [32] along the beam path in accelerator facilities such as Heavy Ion Medical Accelerator in Chiba (HIMAC), Japan [33]. Other targets, Al, C with density of 2.26 g/cm³, CR-39 with density of 1.31 g/cm³, water (H₂O) with density of 1.0 g/cm³, and polyethylene (CH₂) with density of 0.89 g/cm³ were also investigated to understand the tendency of projectile’s σ_ipc for both the ¹²C and ⁴He ion beams. The target thickness was considered 0.5 mm. The simulation was performed for 1 million particles in each energy for each interaction so that the statistical error of the calculated quantity remains less than 2%. The following Fig. 1A shows the simulation setup for ¹²C and PMMA interaction at 135 MeV/n with a target thickness of 0.5 mm, and the beam radius was 5 cm during the simulation. Due to the better visualization, the beam of a 2 cm radius has been visualized in this figure. Fig. 1B shows the travelling of the ¹²C ion beam through the PMMA.

1. Calculation of Projectile’s Isotope Production Cross-Section

The track detection mechanism of track detectors, such as CR-39 is based on the incident ion’s linear energy transfer (LET) inside this detector. The LET threshold and LET resolution of a CR-39 (TD-1 type) detector are approximately 5 keV/μm and 1 keV/μm, respectively. Fig. 2A shows the LET as a function of energy for ¹¹C, ¹²C, and ¹³C in CR-39. It can be observed in the Fig. 2A that the difference in LET among these isotopes is insignificant. As shown in Fig. 2B, the average difference in LET between ¹²C and ¹¹C (LET_C–₁₂–LET_C–₁₁) and that between ¹²C and ¹³C (LET_C–₁₂–LET_C–₁₃) is approximately 0.03 keV/μm. Hence, it is difficult to differentiate the projectile ¹²C ion from its isotopes by a CR-39 track detector. The same is valid for the ⁴He ion beam and its isotopes. However, those estimated values can be effective for the real experiment by simulating the production cross-section of these projectile isotopes.

The production of C and He isotopes from their projectiles can be assessed from the total neutron changing cross-section of the projectile. It can be defined as the probability of production of all the isotopes via the addition (removal) of one or more neutrons to (from) a projectile nucleus [29]. The equation for the projectile’s istotopes production cross-sections, σ_ipc is as follows [34]:

(1)

σipc=-MTρNAxln (Nin-NncNin)

where, N_A is the Avogadro number, N_in is the number of incoming particles, and N_nc is the number of interactions in which an isotope has been produced by the change of neutron(s). M_T, ρ, and x are the molar mass, density, and thickness of the target, respectively. Thus, the production cross-section of a specific isotope (e.g., ¹¹C) is

(2)

σC-11=-MTρNAxln (Nin-NC-11Nin)

where, N_C_–11 is the total number of interactions in which the mass of the projectile changed to that of ¹¹C by the removal of neutron. Thus, the total isotope production cross-section (σ_Tipc) is the sum of the production cross-sections of all types of isotopes. That is,

(3)

σTipc=∑n=915σC-n

where, n is the mass number, which defines the specific isotopes. We cannot distinguish the isotopes of a projectile by experimental measurement using a track detector because of the low mass resolution. Consequently, the total production cross-section of projectile isotopes is likely to be measured simultaneously during the measurement of the charge changing cross-section, and it is equivalent to the mass changing cross-section.

Thus, we calculated the production cross-sections of isotopes of projectiles using PHITS by identifying the event-by-event interactions of projectiles with the target while changing their neutron (N_nc).

Results and Discussion

1. Flux of Projectile’s Isotopes along Beam Path

The transport of ¹²C and ⁴He ion beams of 135, 290, and 400 MeV/n having a diameter of 5 cm through the materials (Ta, Al, and PMMA) of 0.5 mm thickness along the beam path has been simulated. We applied PHITS for this simulation to assess the beam contamination by the projectile’s isotopes produced in the beam path. These energies are in the therapeutic region provided by the HIMAC. Fig. 3A and 3B show the flux of isotopes as a function of energy in the PMMA for ¹²C ion beams of 135 and 400 MeV/n, respectively. The figures reveal that ⁹C, ¹³C, ¹⁴C, and ¹⁵C have significantly low energy with the least flux. Hence, these are too insignificant to be considered because it is highly challenging to reach the target. Only the ¹⁰C, ¹¹C, and ¹³C isotopes contribute significantly through their higher flux and energy for the contamination of the beam and results of cross-section measurements. It can also be observed that the production of these C isotopes is higher at lower energy. In Fig. 3, we can see that the production of isotopes is higher at 135 MeV/n than 400 MeV/n in the same target, PMMA. This may substantially influence the beam purity before the target is reached. It is also found that ³He and ⁶He are the significant isotopes from the ⁴He ion beam that are produced along the beam path for the same interacting materials at the same energies, as shown in Fig. 3C and 3D.

2. Projectile’s Isotope Production Cross-Sections

1) Carbon projectile isotopes

Each interaction of the projectile from which the projectile’s isotopes (⁹C–¹⁵C) can be produced was identified separately using the [T-userdefined] tally of PHITS. Then, the production cross-section of specific projectile’s isotopes was calculated from the number of specific interactions using Equation (2). Table 1 shows the σ_ipc for specific projectile’s isotopes (⁹C–¹⁵C) for different energies in the materials along the beam path of the accelerator system. It can be observed that ¹⁰C and ¹¹C have the maximum production probabilities in each material. The value enclosed in parentheses shows the uncertainty calculated according to the error propagation.

The production probabilities of different isotopes in certain target materials, such as Al, C, CR-39, H₂O, and CH₂, were calculated in this study to understand the trend, and these are shown in Fig. 4. ¹⁰C, ¹¹C, and ¹³C are the most producible isotopes in all the target materials, as observed from these figures and Table 1, which represent the isotopes of the projectile in the materials along the beam path. It is observed that ¹⁰C, ¹¹C, and ¹³C have a significantly higher cross-section in PMMA, H₂O, and CH₂ than other targets. The production cross-section of ¹¹C was significantly higher than that of ¹⁰C and ¹³C in all the targets.

The calculated production cross-sections of ¹⁰C and ¹¹C were compared with the experimental results, as shown in Fig. 5. The experimental results were collected from the references [35–39]. In Fig. 5, the circles and squares indicate the experimental production cross-sections of ¹⁰C and ¹¹C, respectively, for ¹²C and C interaction. The blue and orange colored dashed lines indicate the production cross-sections calculated by PHITS for ¹⁰C and ¹¹C, respectively, for the same interaction. The calculation process and equation can reproduce the trend of the experimental results within the acceptable range, as observed in Fig. 5.

2) Helium projectile isotopes

In this study, the production cross-section of the projectile’s isotopes for a ⁴He ion beam has also been analyzed for the aforementioned target materials as well as for the material along the beam path. During the interaction with the target materials, the produced projectile isotopes from the ⁴He ion beam are ³He and ⁶He. The following Table 2 shows the production cross-sections of these He isotopes during the interaction with material along the beam path at the nominal energies 135, 290, and 400 MeV/n through the materials Ta, Al, and PMMA.

Fig. 6A shows the production cross-sections of He isotope in other target materials. This figure shows the produced He isotopes during the interaction of ⁴He and C at 80 MeV/n. ³He is the most significant projectile isotope that is produced and can play an important role during the measurement of charge changing cross-section with track detectors. The production cross-section of ³He isotopes has been calculated and compared for different targets, as shown in Fig. 6B. It is found that for both H₂O and CH₂, ³He has the highest production cross-section.

Conclusion

Accelerator-based ion beam has an important role in many branches of physics, including heavy ion cancer therapy, the study of heavy ion interaction, etc. When the beam of a projectile is going through the material before reaching the target, the projectile’s isotopes could be produced, which may contaminate the beam due to the material along the beam path like Ta, Al, range shifter (PMMA), etc. These projectile’s isotopes are one of the main sources of error during the cross-section measurement by the nuclear track detector. There are very few experimental data for the production cross-section of the projectile’s isotope yet. Therefore, we tried to observe the trend of the production cross-section of projectile isotopes for the ¹²C and ⁴He ion beams in the materials (Ta, Al, and PMMA) along the beam path for three nominal beam energies, which are 135, 290, and 400 MeV/n, since these energies are in the therapeutic range provided by the HIMAC. The calculations were performed by the Monte Carlo calculation code, PHITS. It is found that ³He is the most producible projectile’s isotope from the ⁴He ion beam, whereas ¹⁰C, ¹¹C, and ¹³C are the most producible projectile’s isotope from the ¹²C ion beam in these energies. Among the beam materials, Al, Ta, and PMMA, along the beam path, ³He have higher production cross-sections in Al and Ta, whereas ¹⁰C, ¹¹C, and ¹³C have higher production cross-sections in PMMA.

Except for the materials along the beam path, other materials, C, H₂O, CH₂, and CR-39, were considered because of their tissue-like properties to observe the tendency of the projectile’s σ_ipc. It is found that the projectile’s σ_ipc is higher in hydrogenous materials like H₂O and CH₂. It can be concluded that the isotopes ¹⁰C, ¹¹C, and ¹³C from the ¹²C ion beam and ³He from the ⁴He ion beam play an important role in hindering the experimental measurement of the total charge changing cross-section in the Al, C, CR-39, H₂O, and CH₂ targets. These isotopes were higher in flux at lower energies. Carbon-11 (¹¹C) has a much higher production cross-section among the three C projectile isotopes in all the target materials mentioned above.

As determined in this study, the role of these projectile’s isotopes may explain why the experimental result is higher than the calculated result for the σ_TCC, particularly in the lower energy region. Thus, this issue should be addressed effectively to obtain a precise result with minimum uncertainties in an experiment involving an ion beam from an accelerator. The observations of this analysis can be used to minimize the error generated during experiments on heavy ion interactions with track detectors.

Notes

Conflict of Interest

No potential conflict of interest relevant to this article was reported.

Ethical Statement

This article does not contain any studies with human participants or animals performed by any of the authors.

Author Contribution

Conceptualization: Rashed Nizam QM. Formal analysis: all authors. Writing - original draft: Ahmed A, Ahmed I. Writing - review and editing: Rashed Nizam QM. Approval of final manuscript: all authors.

References

1. Yasuda N, Konishi T, Matsumoto K, Yamauchi T, Asuka T, Furusawa Y, et al. Dose distribution of carbon ions in air assessed using imaging plates and ionization chamber. Radiat Meas. 2005;40(2–6):384-388.

2. Nagamatsu A, Casolino M, Larsson O, Ito T, Yasuda N, Kitajo K, et al. Space radiation dosimetry to evaluate the effect of polyethylene shielding in the Russian segment of the international space station. Phys Procedia. 2015;80:25-35.

3. Yasuda N, Uchikawa K, Amemiya K, Watanabe N, Takahashi H, Nakazawa M, et al. Estimation of the latent track size of CR-39 using atomic force microscope. Radiat Meas. 2001;34(1–6):45-49.

4. Luoni F, Horst F, Reidel CA, Quarz A, Bagnale L, Sihver L, et al. Total nuclear reaction cross-section database for radiation protection in space and heavy-ion therapy applications. New J Phys. 2021;23:101201.

5. Tran DT, Ong HJ, Nguyen TT, Tanihata I, Aoi N, Ayyad Y, et al. Charge-changing cross-section measurements of 12–16C at around 45A MeV and development of a Glauber model for incident energies 10A–2100A MeV. Phys Rev C. 2016;94(6):1-9.

6. Evoli C, Gaggero D, Vittino A, Di Mauro M, Grasso D, Mazziotta MN. Cosmic-ray propagation with DRAGON2: II. Nuclear interactions with the interstellar gas. J Cosmol Astropart Phys. 2018;2018:006.

7. Cheshire DL, Huggett RW, Johnson DP, Jones WV, Rountree SP, Verma SD, et al. Fragmentation cross sections of 2.1-GeV/nucleon 12C and 16O ions. Phys Rev D. 1974;10(1):25-31.

8. Westfall GD, Wilson LW, Lindstrom PJ, Crawford HJ, Greiner DE, Heckman HH. Fragmentation of relativistic 56Fe. Phys Rev C. 1979;19(4):1309-1323.

9. Webber WR, Brautigam DA. Fragmentation of 56Fe nuclei on CH2, carbon, and hydrogen targets: individual charge changing and total cross sections. Astrophys J. 1982;260:894-908.

10. Cummings JR, Binns WR, Garrard TL, Israel MH, Klarmann J, Stone EC, et al. Determination of the cross sections for the production of fragments from relativistic nucleus-nucleus interactions. II. Parametric fits. Phys Rev C. 1990;42(6):2530-2545.

11. Lindstrom PJ, Greiner DE, Heckman HH, Cork B, Beiser FS. Fragmentation of 40Ar at 100 GeV/c: volume 7 (HE session). Proceedings from the 14th International Cosmic Ray Conference. 1975 Aug 15–29. Munich, Germany. 2315.

12. Agnes P, Albuquerque IFM, Alexander T, Alton AK, Ave M, Back HO, et al. Measurement of the ion fraction and mobility of 218Po produced in 222Rn decays in liquid argon. J Instrum. 2019;14:P11018.

13. Brechtmann C, Heinrich W. Measurements of elemental fragmentation cross section for relativistic heavy ions using CR39 plastic nuclear track detector. Nucl Instrum Methods Phys Res B. 1988;29(4):675-679.

14. Yasuda N, Yamamoto M, Amemiya K, Takahashi H, Kyan A, Ogura K. Track sensitivity and the surface roughness measurements of CR-39 with atomic force microscope. Radiat Meas. 1999;31(1–6):203-208.

15. Yasuda N, Zhang DH, Kodaira S, Koguchi Y, Takebayashi S, Shinozaki W, et al. Verification of angular dependence for track sensitivity on several types of CR-39. Radiat Meas. 2008;43(Suppl 1):S269-S273.

16. DeWitt JM, Benton ER, Uchihori Y, Yasuda N, Benton EV, Frank AL. Assessment of radiation shielding materials for protection of space crews using CR-39 plastic nuclear track detector. Radiat Meas. 2009;44(9–10):905-908.

17. Golovchenko AN, Sihver L, Ota S, Skvarc J, Yasuda N, Kodaira S, et al. Fragmentation of 370 MeV/n 20Ne and 470 MeV/n 24Mg in light targets. Radiat Meas. 2010;45(7):856-860.

18. Huo LD, Wang LH, Zhu JH, Li HL, Li JS, Kodaira S, et al. The total charge-changing cross sections and the partial cross sections of 56Fe fragmentation on Al, C and CH2 targets. Chin J Phys. 2019;60:88-97.

19. Toshito T, Kodama K, Sihver L, Yusa K, Ozaki M, Amako K, et al. Measurements of total and partial charge-changing cross sections for 200- to 400-MeV/nucleon 12C on water and polycarbonate. Phys Rev C. 2007;75(5):054606.

20. Young DA. Etching of radiation damage in lithium fluoride. Nature. 1958;182(4632):375-377.

21. Price PB, Walker RM. Electron microscope observation of etched tracks from spallation recoils in mica. Phys Rev Lett. 1962;8(5):217.

22. Price PB, Walker RM. Observations of charged-particle tracks in solids. J Appl Phys. 1962;33(12):3400-3406.

23. Kodaira S, Hasebe N, Doke T, Kitagawa A, Kitamura H, Sato S, et al. Mass resolution for iron isotopes in CR-39 track detector. Jpn J Appl Phys. 2004;43(9R):6358-6363.

24. Hayashi T, Hamasaki R, Doke T. Mass resolution for iron isotopes in the plastic CR-39. Nucl Tracks Radiat Meas. 1982;6(1):1-7.

25. Wang J, Toloczko MB, Kruska K, Schreiber DK, Edwards DJ, Zhu Z, et al. Carbon contamination during ion irradiation: accurate detection and characterization of its effect on microstructure of ferritic/martensitic steels. Sci Rep. 2017;7(1):15813.

26. Kozma P, Tolstov KD, Yanovsky VV. Cross sections for the production of 11C in C targets by 3.65 A GeV projectiles. Nucl Instrum Methods Phys Res A. 1990;291(3):662-663.

27. Kaki K. Reaction cross sections of proton scattering from carbon isotopes (A=8-22 by means of the relativistic impulse approximation. Prog Theor Exp Phys. 2017;2017(9):ptx116.

28. Sato T, Niita K, Matsuda N, Hashimoto S, Iwamoto Y, Furuta T, et al. Overview of particle and heavy ion transport code system PHITS. Ann Nucl Energy. 2015;82:110-115.

29. Horst F, Schuy C, Weber U, Brinkmann KT, Zink K. Measurement of charge- and mass-changing cross sections for 4He+12C collisions in the energy range 80–220 MeV/u for applications in ion beam therapy. Phys Rev C. 2017;96(2):024624.

30. Ogawa T, Sato T, Hashimoto S, Satoh D, Tsuda S, Niita K. Energy-dependent fragmentation cross sections of relativistic 12C. Phys Rev C. 2015;92(2):024614.

31. Boudard A, Cugnon J, David JC, Leray S, Mancusi D. New potentialities of the Liège intranuclear cascade model for reactions induced by nucleons and light charged particles. Phys Rev C. 2013;87(1):014606.

32. Ploc O, Dachev T, Uchihori Y, Kitamura H, Sihver L. Fragmentation from heavy ion beams in HIMAC BIO room calculated with PHITS and measured with Liulin. Proceedings of the 2017 IEEE Aerospace Conference. 2017 Mar 4–11. Big Sky, MT, USA. 1-10.

33. Iwata Y, Fujita T, Fujimoto T, Furukawa T, Hara Y, Kondo K, et al. Development of carbon-ion radiotherapy facilities at NIRS. IEEE Trans Appl Supercond. 2018;28(3):4400807.

34. Golovchenko AN, Skvarc J, Yasuda N, Giacomelli M, Tretyakova SP, Ilic R, et al. Total charge-changing and partial cross-section measurements in the reactions of ~110–250 MeV/nucleon 12C in carbon, paraffin, and water. Phys Rev C. 2002;66(1):014609.

35. Horst F, Adi W, Aricò G, Brinkmann KT, Durante M, Reidel CA, et al. Measurement of PET isotope production cross sections for protons and carbon ions on carbon and oxygen targets for applications in particle therapy range verification. Phys Med Biol. 2019;64(20):205012.

36. Kidd JM, Lindstrom PJ, Crawford HJ, Woods G. Fragmentation of carbon ions at 250 MeV/nucleon. Phys Rev C. 1988;37(6):2613-2623.

37. Webber WR, Kish JC, Schrier DA. Individual charge changing fragmentation cross sections of relativistic nuclei in hydrogen, helium, and carbon targets. Phys Rev C. 1990;41(2):533-546.

38. Yashima H, Uwamino Y, Iwase H, Sugita H, Nakamura T, Ito S, et al. Measurement and calculation of radioactivities of spallation products by high-energy heavy ions. Radiochim Acta. 2003;91(12):689-696.

39. Boillos JM, Cortina-Gil D, Benlliure J, Rodriguez-Sanchez JL, Alvarez-Pol H, Atar L, et al. Isotopic cross sections of fragmentation residues produced by light projectiles on carbon near. Phys Rev C. 2022;105(1):014611.

Fig. 1

(A) The simulation set up for the ¹²C and PMMA interaction at 135 MeV/n with the target thickness of 0.5 mm. For better visualization, the beam of a 2-cm radius has been grabbed in this figure, whereas in real situations, it was 5 cm in diameter. (B) The travelling of the ¹²C ion beam through the PMMA. PMMA, polymethyl methacrylate.

Fig. 2

(A) A comparison of the linear energy transfer (LET [keV/μm]) of the three main isotopes of ¹²C projectiles in CR-39 as a function of energy (E [MeV/n]). We can observe that the LET value of each isotope at a specific energy is largely equal to that of ¹²C. (B) The distribution of the differences in LET between ¹²C and its isotopes ¹¹C and ¹³C. The average difference in LET between ¹²C and ¹¹C, (LET_C_–12–LET_C_–11) and between ¹²C and ¹³C (LET_C_–12–LET_C_–13) is approximately −0.03 keV/μm.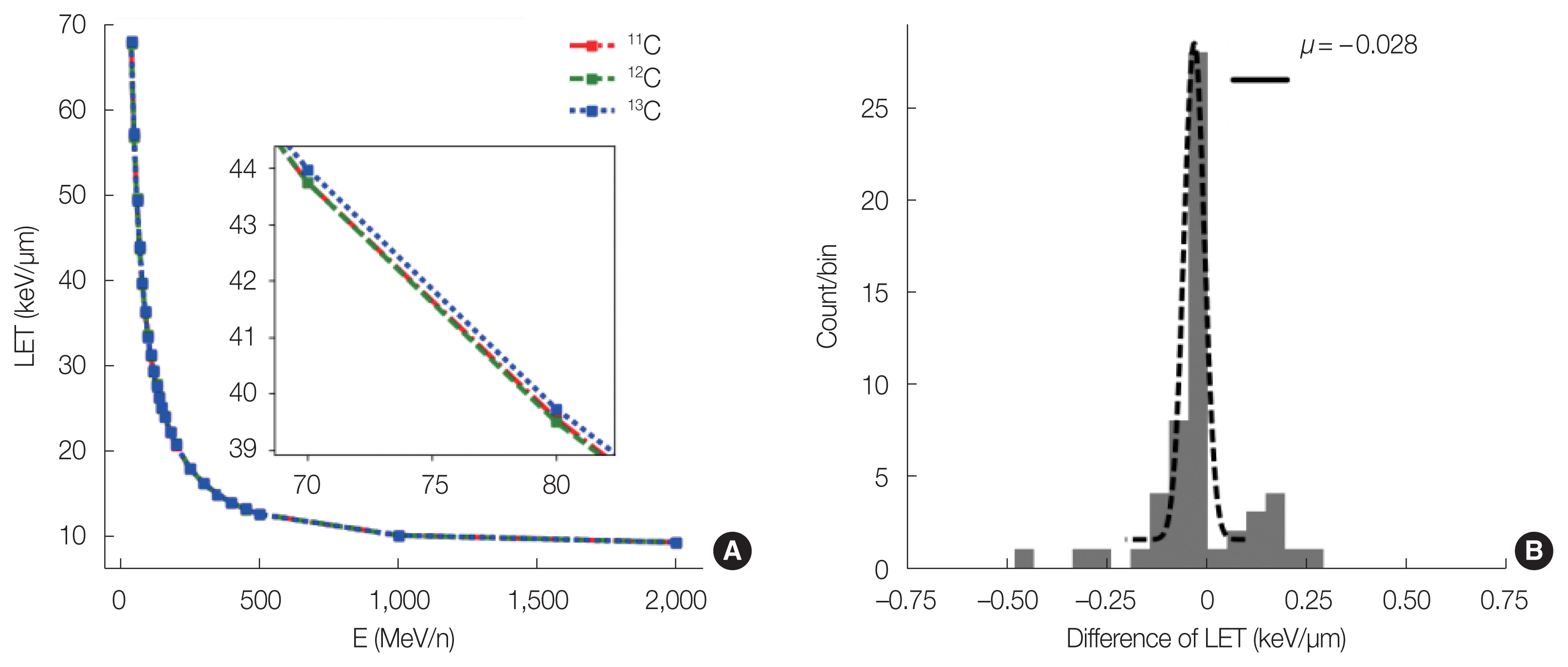

Fig. 3

(A) The flux of isotopes as a function of energy in the PMMA along the beam path for the ¹²C ion beam of 135 MeV/n. (B) The same for the ¹²C ion beam of 400 MeV/n. (C, D) The same for ⁴He and PMMA interactions, from where it is seen that ³He and ⁶He are the significant isotopes for the ⁴He ion beam. PMMA, polymethyl methacrylate.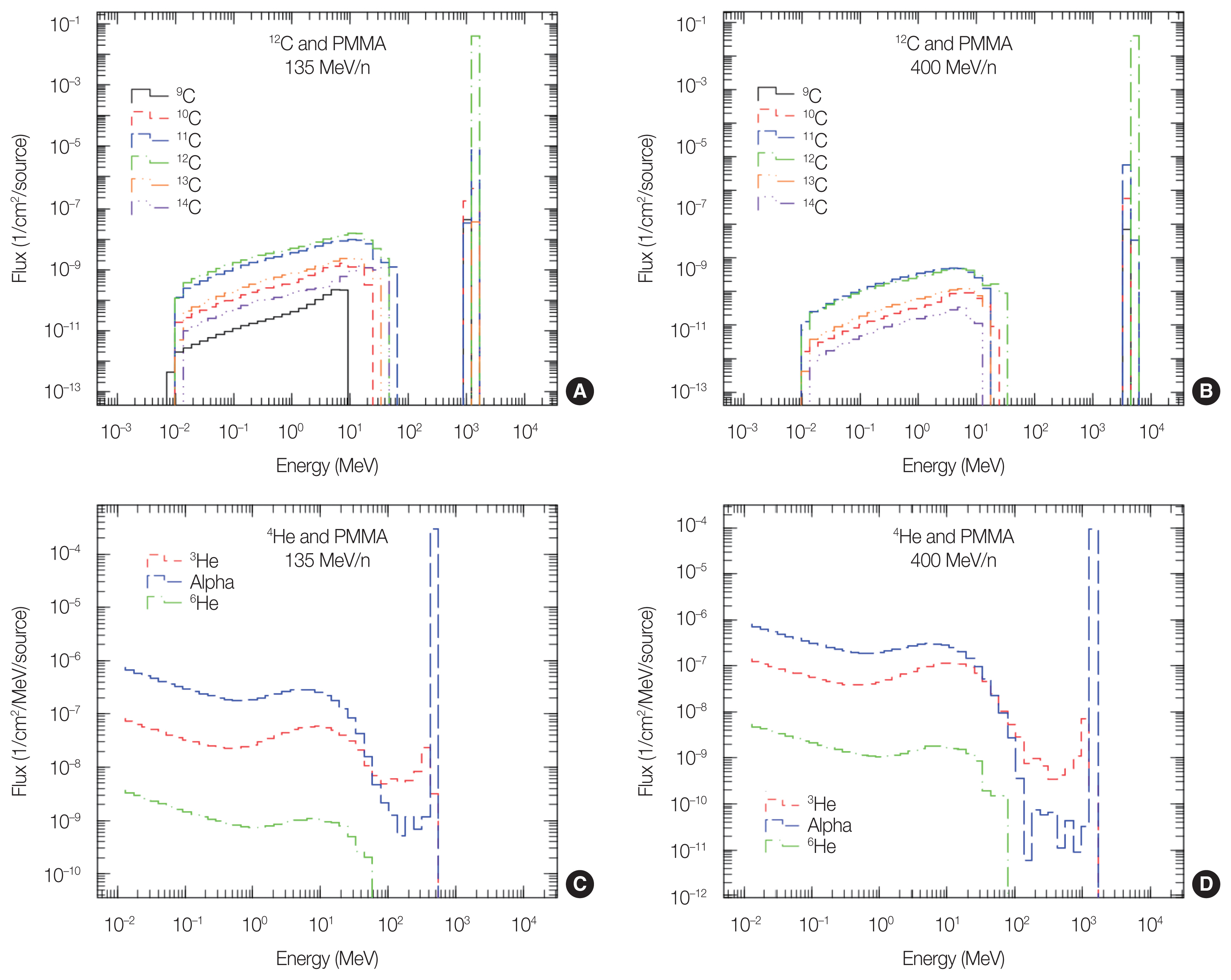

Fig. 4

The production cross-sections of ¹⁰C, ¹¹C, and ¹³C in different target materials are shown in (A, B, C), respectively. The descending order of production cross-section of ¹⁰C in different targets is H₂O>CH₂>C>Al>CR-39. The same for ¹¹C is H₂O>CH₂>C>CR-39>Al. The same for ¹³C is H₂O>Al>CR-39>C>CH₂. Carbon-11 (¹¹C) has a higher production cross-section than ¹⁰C in all materials.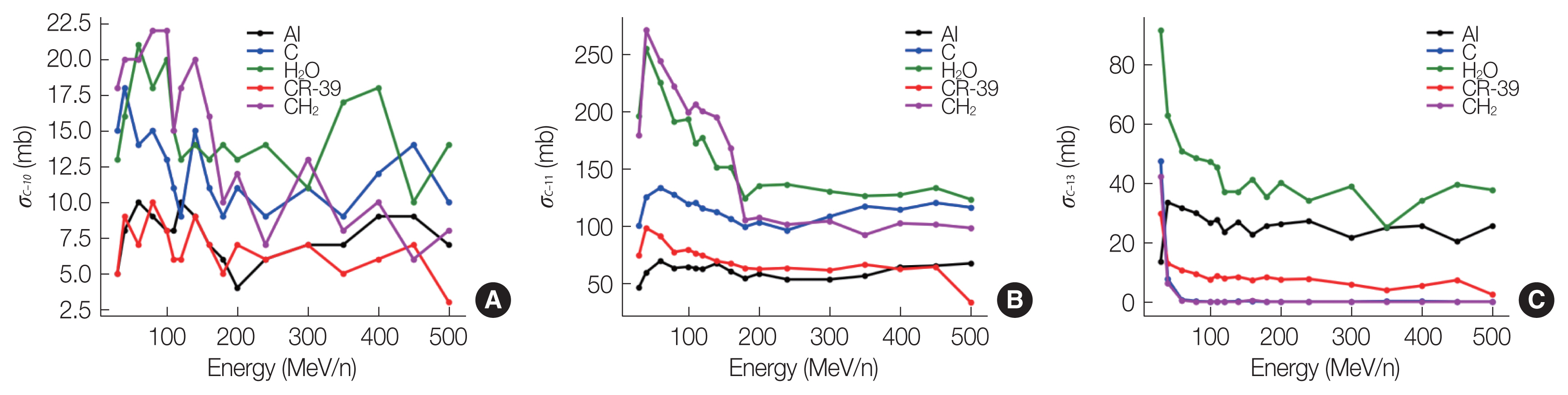

Fig. 5

A comparison between the calculated and experimental production cross-sections of ¹⁰C and ¹¹C for the ¹²C and C interactions. The experimental results have been collected [35–39]. The circles and squares indicate the production cross-sections of ¹⁰C and ¹¹C, respectively. The blue and orange colored dashed lines denote the calculated production cross-sections for ¹⁰C and ¹¹C, respectively. It is observed that the experimental results are in agreement with the calculated results. PHITS, Particle and Heavy Ion Transport code System.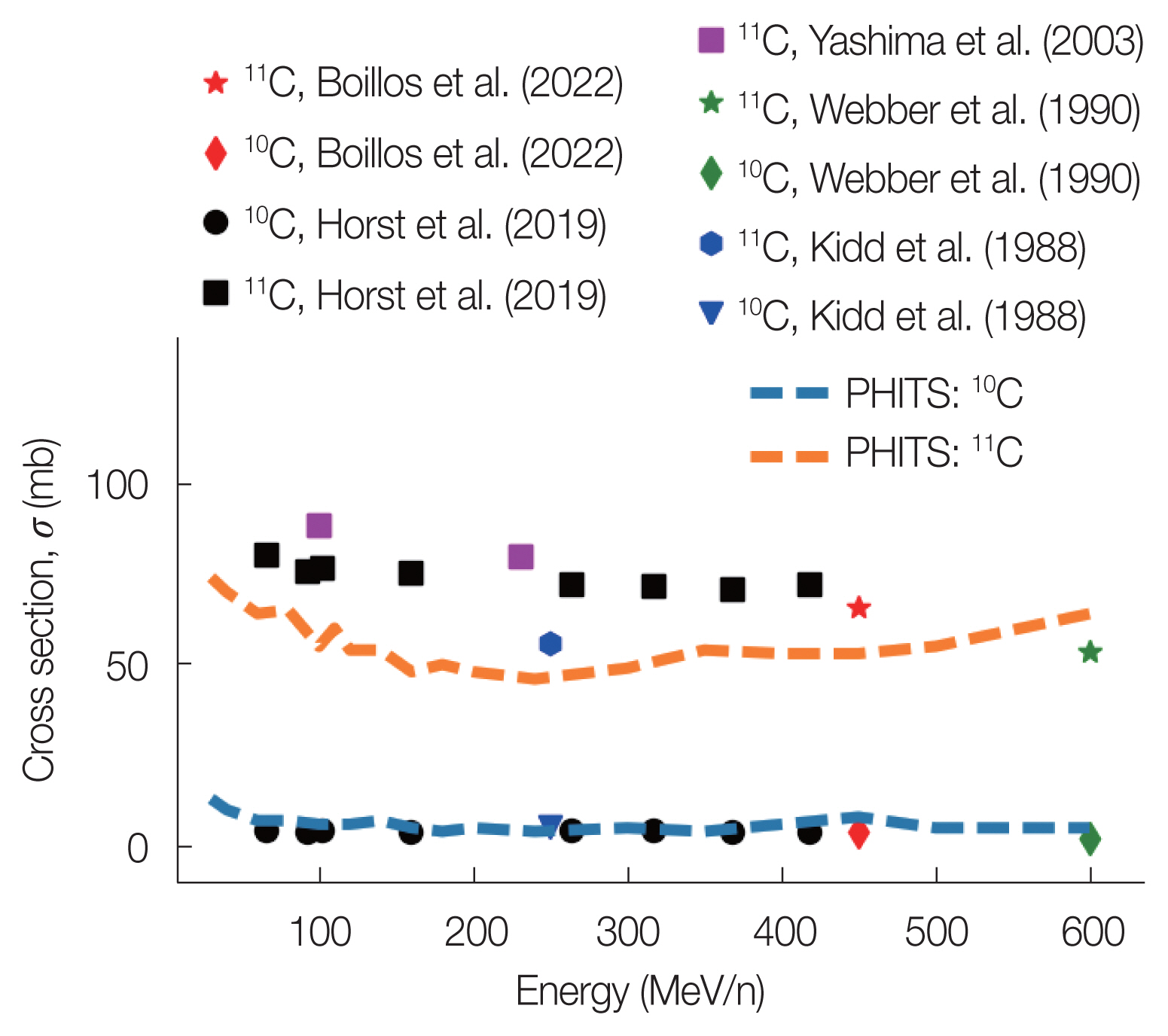

Fig. 6

(A) The flux of the He isotopes produced during the interaction of ⁴He and C at 80 MeV/n, where ³He is significant only. (B) The production cross-section of this ³He isotope in different target materials.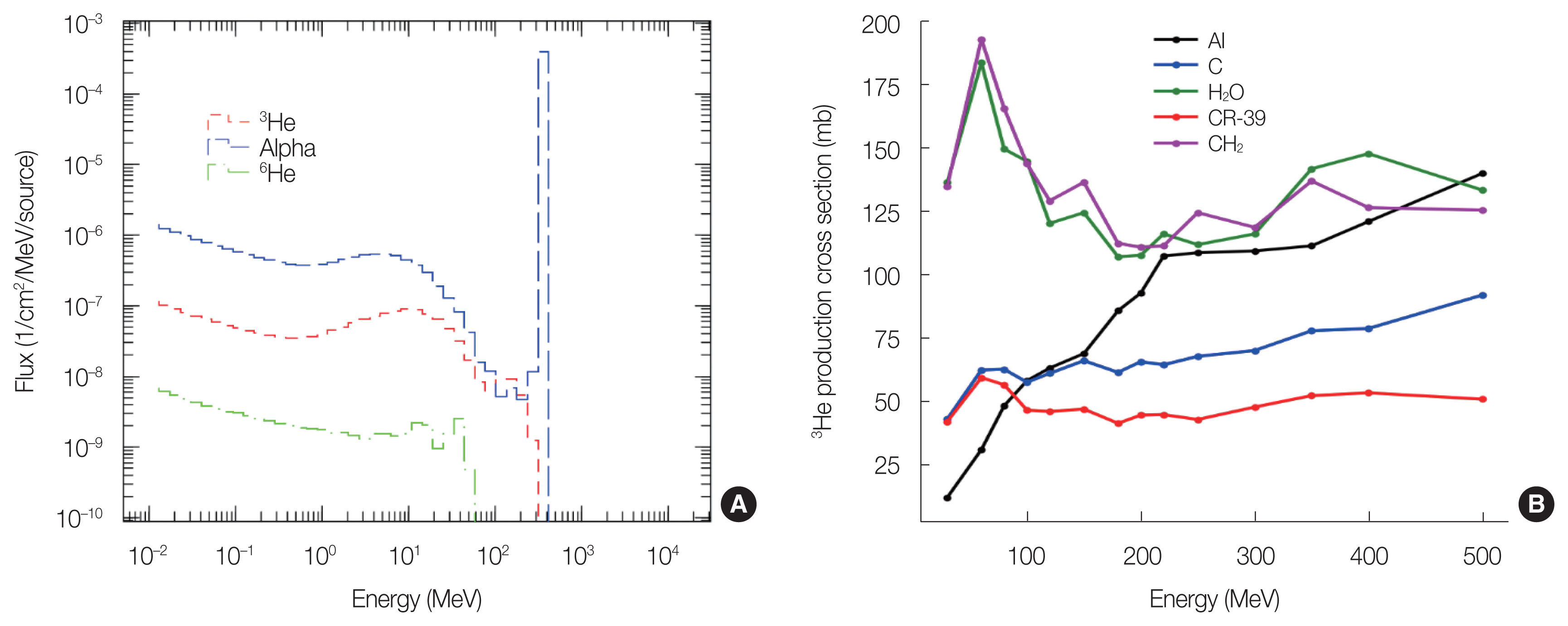

Table 1

Production Cross-Section (mb) of C Isotopes (⁹C–¹⁵C) for Different Energies of ¹²C Ion Beam in Different Materials along the Beam Path

Materials	Energy (MeV/n)

	Ta			Al			PMMA

	135	290	400	135	290	400	135	290	400
Production cross-section (mb)
σ_C_–9	2.2	0.4	0.4	0.3	1.3	0.7	7.0	10.4	7.0
σ_C_–10	2.0	2.0	3.0	8.0	5.0	9.0	89.0	75.0	77.0
σ_C_–11	45.0	39.0	35.0	70.0	59.0	64.0	949.0	763.0	841.0
σ_C_–13	-	0.4	-	31.2	16.9	25.6	59.2	64.4	48.7
σ_C_–14	-	-	-	3.0	4.3	2.3	13.9	13.9	12.2
σ_C_–15	-	-	-	-	-	-	-	-	-
σ_Tipc	49.2 (1.1)	41.8 (1.2)	38.4 (1.1)	104.5 (3.1)	86.5 (2.2)	101.6 (3.1)	118.1 (13.6)	926.7 (12.6)	985.9 (12.1)

We can observe that the maximum production probabilities are for ¹⁰C and ¹¹C in each material. The value in parentheses indicates the uncertainty.

PMMA, polymethyl methacrylate; σ_Tipc, total isotope production cross-section.

Table 2

Production Cross-Section (mb) of He Projectile’s Isotopes from ⁴He Ion Beam in Different Materials along the Beam Path for Different Energies

Materials	Energy (MeV/n)

	Ta			Al			PMMA

	135	290	400	135	290	400	135	290	400
Production cross-section (mb)
σ_He–3	71.3	170.9	263.4	67.2	97.3	126.8	673.3	680.2	762.1
σ_He–6	7.0	22.0	32.0	2.0	3.0	4.0	9.0	12.0	12.0
σ_Tipc	78.3 (1.1)	192.9 (4.2)	295.4 (5.1)	69.2 (1.1)	100.3 (2.2)	130.8 (1.1)	682.3 (13.6)	692.2 (12.6)	774.1 (12.1)

The maximum production probability is for ³He in each material. The value in parentheses indicates the uncertainty.

PMMA, polymethyl methacrylate; σ_Tipc, total projectile isotope production cross-section.